Jonathan J Deeks, Julian PT Higgins, Douglas G Altman; on behalf of the Cochrane Statistical Methods Group
Key Points:
- Meta-analysis is the statistical combination of results from two or more separate studies.
- Potential advantages of meta-analyses include an improvement in precision, the ability to answer questions not posed by individual studies, and the opportunity to settle controversies arising from conflicting claims. However, they also have the potential to mislead seriously, particularly if specific study designs, within-study biases, variation across studies, and reporting biases are not carefully considered.
- It is important to be familiar with the type of data (e.g. dichotomous, continuous) that result from measurement of an outcome in an individual study, and to choose suitable effect measures for comparing intervention groups.
- Most meta-analysis methods are variations on a weighted average of the effect estimates from the different studies.
- Studies with no events contribute no information about the risk ratio or odds ratio. For rare events, the Peto method has been observed to be less biased and more powerful than other methods.
- Variation across studies (heterogeneity) must be considered, although most Cochrane Reviews do not have enough studies to allow for the reliable investigation of its causes. Random-effects meta-analyses allow for heterogeneity by assuming that underlying effects follow a normal distribution, but they must be interpreted carefully. Prediction intervals from random-effects meta-analyses are a useful device for presenting the extent of between-study variation.
- Many judgements are required in the process of preparing a meta-analysis. Sensitivity analyses should be used to examine whether overall findings are robust to potentially influential decisions.
Cite this chapter as: Deeks JJ, Higgins JPT, Altman DG (editors). Chapter 10: Analysing data and undertaking meta-analyses. In: Higgins JPT, Thomas J, Chandler J, Cumpston M, Li T, Page MJ, Welch VA (editors). Cochrane Handbook for Systematic Reviews of Interventions version 6.3 (updated February 2022). Cochrane, 2022. Available from www.training.cochrane.org/handbook.
10.1 Do not start here!
It can be tempting to jump prematurely into a statistical analysis when undertaking a systematic review. The production of a diamond at the bottom of a plot is an exciting moment for many authors, but results of meta-analyses can be very misleading if suitable attention has not been given to formulating the review question; specifying eligibility criteria; identifying and selecting studies; collecting appropriate data; considering risk of bias; planning intervention comparisons; and deciding what data would be meaningful to analyse. Review authors should consult the chapters that precede this one before a meta-analysis is undertaken.
10.2 Introduction to meta-analysis 
| Update to this section pending |
An important step in a systematic review is the thoughtful consideration of whether it is appropriate to combine the numerical results of all, or perhaps some, of the studies. Such a meta-analysis yields an overall statistic (together with its confidence interval) that summarizes the effectiveness of an experimental intervention compared with a comparator intervention. Potential advantages of meta-analyses include the following:
- To improve precision. Many studies are too small to provide convincing evidence about intervention effects in isolation. Estimation is usually improved when it is based on more information.
- To answer questions not posed by the individual studies. Primary studies often involve a specific type of participant and explicitly defined interventions. A selection of studies in which these characteristics differ can allow investigation of the consistency of effect across a wider range of populations and interventions. It may also, if relevant, allow reasons for differences in effect estimates to be investigated.
- To settle controversies arising from apparently conflicting studies or to generate new hypotheses. Statistical synthesis of findings allows the degree of conflict to be formally assessed, and reasons for different results to be explored and quantified.
Of course, the use of statistical synthesis methods does not guarantee that the results of a review are valid, any more than it does for a primary study. Moreover, like any tool, statistical methods can be misused.
This chapter describes the principles and methods used to carry out a meta-analysis for a comparison of two interventions for the main types of data encountered. The use of network meta-analysis to compare more than two interventions is addressed in Chapter 11. Formulae for most of the methods described are provided in a supplementary document ‘Statistical algorithms in Review Manager’ (available via the Handbook web pages), and a longer discussion of many of the issues is available (Deeks et al 2001).
10.2.1 Principles of meta-analysis
The commonly used methods for meta-analysis follow the following basic principles:
- Meta-analysis is typically a two-stage process. In the first stage, a summary statistic is calculated for each study, to describe the observed intervention effect in the same way for every study. For example, the summary statistic may be a risk ratio if the data are dichotomous, or a difference between means if the data are continuous (see Chapter 6).
-
In the second stage, a summary (combined) intervention effect estimate is calculated as a weighted average of the intervention effects estimated in the individual studies. A weighted average is defined as
where Yi is the intervention effect estimated in the ith study, Wi is the weight given to the ith study, and the summation is across all studies. Note that if all the weights are the same then the weighted average is equal to the mean intervention effect. The bigger the weight given to the ith study, the more it will contribute to the weighted average (see Section 10.3).
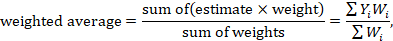
- The combination of intervention effect estimates across studies may optionally incorporate an assumption that the studies are not all estimating the same intervention effect, but estimate intervention effects that follow a distribution across studies. This is the basis of a random-effects meta-analysis (see Section 10.10.4). Alternatively, if it is assumed that each study is estimating exactly the same quantity, then a fixed-effect meta-analysis is performed.
- The standard error of the summary intervention effect can be used to derive a confidence interval, which communicates the precision (or uncertainty) of the summary estimate; and to derive a P value, which communicates the strength of the evidence against the null hypothesis of no intervention effect.
- As well as yielding a summary quantification of the intervention effect, all methods of meta-analysis can incorporate an assessment of whether the variation among the results of the separate studies is compatible with random variation, or whether it is large enough to indicate inconsistency of intervention effects across studies (see Section 10.10).
- The problem of missing data is one of the numerous practical considerations that must be thought through when undertaking a meta-analysis. In particular, review authors should consider the implications of missing outcome data from individual participants (due to losses to follow-up or exclusions from analysis) (see Section 10.12).
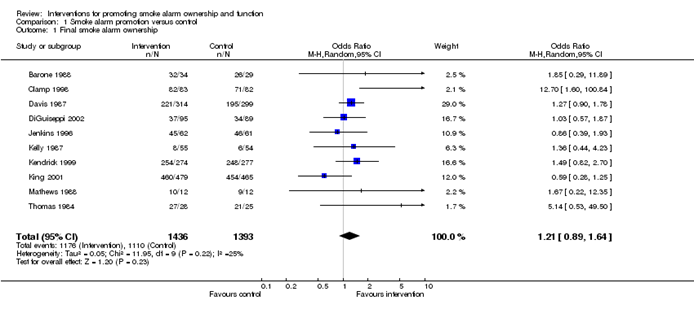
Meta-analyses are usually illustrated using a forest plot. An example appears in Figure 10.2.a. A forest plot displays effect estimates and confidence intervals for both individual studies and meta-analyses (Lewis and Clarke 2001). Each study is represented by a block at the point estimate of intervention effect with a horizontal line extending either side of the block. The area of the block indicates the weight assigned to that study in the meta-analysis while the horizontal line depicts the confidence interval (usually with a 95% level of confidence). The area of the block and the confidence interval convey similar information, but both make different contributions to the graphic. The confidence interval depicts the range of intervention effects compatible with the study’s result. The size of the block draws the eye towards the studies with larger weight (usually those with narrower confidence intervals), which dominate the calculation of the summary result, presented as a diamond at the bottom.
Figure 10.2.a Example of a forest plot from a review of interventions to promote ownership of smoke alarms (DiGuiseppi and Higgins 2001). Reproduced with permission of John Wiley & Sons
10.3 A generic inverse-variance approach to meta-analysis
A very common and simple version of the meta-analysis procedure is commonly referred to as the inverse-variance method. This approach is implemented in its most basic form in RevMan, and is used behind the scenes in many meta-analyses of both dichotomous and continuous data.
The inverse-variance method is so named because the weight given to each study is chosen to be the inverse of the variance of the effect estimate (i.e. 1 over the square of its standard error). Thus, larger studies, which have smaller standard errors, are given more weight than smaller studies, which have larger standard errors. This choice of weights minimizes the imprecision (uncertainty) of the pooled effect estimate.
10.3.1 Fixed-effect method for meta-analysis
A fixed-effect meta-analysis using the inverse-variance method calculates a weighted average as:
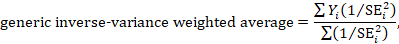
where Yi is the intervention effect estimated in the ith study, SEi is the standard error of that estimate, and the summation is across all studies. The basic data required for the analysis are therefore an estimate of the intervention effect and its standard error from each study. A fixed-effect meta-analysis is valid under an assumption that all effect estimates are estimating the same underlying intervention effect, which is referred to variously as a ‘fixed-effect’ assumption, a ‘common-effect’ assumption or an ‘equal-effects’ assumption. However, the result of the meta-analysis can be interpreted without making such an assumption (Rice et al 2018).
10.3.2 Random-effects methods for meta-analysis
A variation on the inverse-variance method is to incorporate an assumption that the different studies are estimating different, yet related, intervention effects (Higgins et al 2009). This produces a random-effects meta-analysis, and the simplest version is known as the DerSimonian and Laird method (DerSimonian and Laird 1986). Random-effects meta-analysis is discussed in detail in Section 10.10.4.
10.3.3 Performing inverse-variance meta-analyses
Most meta-analysis programs perform inverse-variance meta-analyses. Usually the user provides summary data from each intervention arm of each study, such as a 2×2 table when the outcome is dichotomous (see Chapter 6, Section 6.4), or means, standard deviations and sample sizes for each group when the outcome is continuous (see Chapter 6, Section 6.5). This avoids the need for the author to calculate effect estimates, and allows the use of methods targeted specifically at different types of data (see Sections 10.4 and 10.5).
When the data are conveniently available as summary statistics from each intervention group, the inverse-variance method can be implemented directly. For example, estimates and their standard errors may be entered directly into RevMan under the ‘Generic inverse variance’ outcome type. For ratio measures of intervention effect, the data must be entered into RevMan as natural logarithms (for example, as a log odds ratio and the standard error of the log odds ratio). However, it is straightforward to instruct the software to display results on the original (e.g. odds ratio) scale. It is possible to supplement or replace this with a column providing the sample sizes in the two groups. Note that the ability to enter estimates and standard errors creates a high degree of flexibility in meta-analysis. It facilitates the analysis of properly analysed crossover trials, cluster-randomized trials and non-randomized trials (see Chapter 23), as well as outcome data that are ordinal, time-to-event or rates (see Chapter 6).
10.4 Meta-analysis of dichotomous outcomes
There are four widely used methods of meta-analysis for dichotomous outcomes, three fixed-effect methods (Mantel-Haenszel, Peto and inverse variance) and one random-effects method (DerSimonian and Laird inverse variance). All of these methods are available as analysis options in RevMan. The Peto method can only combine odds ratios, whilst the other three methods can combine odds ratios, risk ratios or risk differences. Formulae for all of the meta-analysis methods are available elsewhere (Deeks et al 2001).
Note that having no events in one group (sometimes referred to as ‘zero cells’) causes problems with computation of estimates and standard errors with some methods: see Section 10.4.4.
10.4.1 Mantel-Haenszel methods
When data are sparse, either in terms of event risks being low or study size being small, the estimates of the standard errors of the effect estimates that are used in the inverse-variance methods may be poor. Mantel-Haenszel methods are fixed-effect meta-analysis methods using a different weighting scheme that depends on which effect measure (e.g. risk ratio, odds ratio, risk difference) is being used (Mantel and Haenszel 1959, Greenland and Robins 1985). They have been shown to have better statistical properties when there are few events. As this is a common situation in Cochrane Reviews, the Mantel-Haenszel method is generally preferable to the inverse variance method in fixed-effect meta-analyses. In other situations the two methods give similar estimates.
10.4.2 Peto odds ratio method
Peto’s method can only be used to combine odds ratios (Yusuf et al 1985). It uses an inverse-variance approach, but uses an approximate method of estimating the log odds ratio, and uses different weights. An alternative way of viewing the Peto method is as a sum of ‘O – E’ statistics. Here, O is the observed number of events and E is an expected number of events in the experimental intervention group of each study under the null hypothesis of no intervention effect.
The approximation used in the computation of the log odds ratio works well when intervention effects are small (odds ratios are close to 1), events are not particularly common and the studies have similar numbers in experimental and comparator groups. In other situations it has been shown to give biased answers. As these criteria are not always fulfilled, Peto’s method is not recommended as a default approach for meta-analysis.
Corrections for zero cell counts are not necessary when using Peto’s method. Perhaps for this reason, this method performs well when events are very rare (Bradburn et al 2007); see Section 10.4.4.1. Also, Peto’s method can be used to combine studies with dichotomous outcome data with studies using time-to-event analyses where log-rank tests have been used (see Section 10.9).
10.4.3 Which effect measure for dichotomous outcomes?
Effect measures for dichotomous data are described in Chapter 6, Section 6.4.1. The effect of an intervention can be expressed as either a relative or an absolute effect. The risk ratio (relative risk) and odds ratio are relative measures, while the risk difference and number needed to treat for an additional beneficial outcome are absolute measures. A further complication is that there are, in fact, two risk ratios. We can calculate the risk ratio of an event occurring or the risk ratio of no event occurring. These give different summary results in a meta-analysis, sometimes dramatically so.
The selection of a summary statistic for use in meta-analysis depends on balancing three criteria (Deeks 2002). First, we desire a summary statistic that gives values that are similar for all the studies in the meta-analysis and subdivisions of the population to which the interventions will be applied. The more consistent the summary statistic, the greater is the justification for expressing the intervention effect as a single summary number. Second, the summary statistic must have the mathematical properties required to perform a valid meta-analysis. Third, the summary statistic would ideally be easily understood and applied by those using the review. The summary intervention effect should be presented in a way that helps readers to interpret and apply the results appropriately. Among effect measures for dichotomous data, no single measure is uniformly best, so the choice inevitably involves a compromise.
Consistency Empirical evidence suggests that relative effect measures are, on average, more consistent than absolute measures (Engels et al 2000, Deeks 2002, Rücker et al 2009). For this reason, it is wise to avoid performing meta-analyses of risk differences, unless there is a clear reason to suspect that risk differences will be consistent in a particular clinical situation. On average there is little difference between the odds ratio and risk ratio in terms of consistency (Deeks 2002). When the study aims to reduce the incidence of an adverse event, there is empirical evidence that risk ratios of the adverse event are more consistent than risk ratios of the non-event (Deeks 2002). Selecting an effect measure based on what is the most consistent in a particular situation is not a generally recommended strategy, since it may lead to a selection that spuriously maximizes the precision of a meta-analysis estimate.
Mathematical properties The most important mathematical criterion is the availability of a reliable variance estimate. The number needed to treat for an additional beneficial outcome does not have a simple variance estimator and cannot easily be used directly in meta-analysis, although it can be computed from the meta-analysis result afterwards (see Chapter 15, Section 15.4.2). There is no consensus regarding the importance of two other often-cited mathematical properties: the fact that the behaviour of the odds ratio and the risk difference do not rely on which of the two outcome states is coded as the event, and the odds ratio being the only statistic which is unbounded (see Chapter 6, Section 6.4.1).
Ease of interpretation The odds ratio is the hardest summary statistic to understand and to apply in practice, and many practising clinicians report difficulties in using them. There are many published examples where authors have misinterpreted odds ratios from meta-analyses as risk ratios. Although odds ratios can be re-expressed for interpretation (as discussed here), there must be some concern that routine presentation of the results of systematic reviews as odds ratios will lead to frequent over-estimation of the benefits and harms of interventions when the results are applied in clinical practice. Absolute measures of effect are thought to be more easily interpreted by clinicians than relative effects (Sinclair and Bracken 1994), and allow trade-offs to be made between likely benefits and likely harms of interventions. However, they are less likely to be generalizable.
It is generally recommended that meta-analyses are undertaken using risk ratios (taking care to make a sensible choice over which category of outcome is classified as the event) or odds ratios. This is because it seems important to avoid using summary statistics for which there is empirical evidence that they are unlikely to give consistent estimates of intervention effects (the risk difference), and it is impossible to use statistics for which meta-analysis cannot be performed (the number needed to treat for an additional beneficial outcome). It may be wise to plan to undertake a sensitivity analysis to investigate whether choice of summary statistic (and selection of the event category) is critical to the conclusions of the meta-analysis (see Section 10.14).
It is often sensible to use one statistic for meta-analysis and to re-express the results using a second, more easily interpretable statistic. For example, often meta-analysis may be best performed using relative effect measures (risk ratios or odds ratios) and the results re-expressed using absolute effect measures (risk differences or numbers needed to treat for an additional beneficial outcome – see Chapter 15, Section 15.4. This is one of the key motivations for ‘Summary of findings’ tables in Cochrane Reviews: see Chapter 14). If odds ratios are used for meta-analysis they can also be re-expressed as risk ratios (see Chapter 15, Section 15.4). In all cases the same formulae can be used to convert upper and lower confidence limits. However, all of these transformations require specification of a value of baseline risk that indicates the likely risk of the outcome in the ‘control’ population to which the experimental intervention will be applied. Where the chosen value for this assumed comparator group risk is close to the typical observed comparator group risks across the studies, similar estimates of absolute effect will be obtained regardless of whether odds ratios or risk ratios are used for meta-analysis. Where the assumed comparator risk differs from the typical observed comparator group risk, the predictions of absolute benefit will differ according to which summary statistic was used for meta-analysis.
10.4.4 Meta-analysis of rare events
For rare outcomes, meta-analysis may be the only way to obtain reliable evidence of the effects of healthcare interventions. Individual studies are usually under-powered to detect differences in rare outcomes, but a meta-analysis of many studies may have adequate power to investigate whether interventions do have an impact on the incidence of the rare event. However, many methods of meta-analysis are based on large sample approximations, and are unsuitable when events are rare. Thus authors must take care when selecting a method of meta-analysis (Efthimiou 2018).
There is no single risk at which events are classified as ‘rare’. Certainly risks of 1 in 1000 constitute rare events, and many would classify risks of 1 in 100 the same way. However, the performance of methods when risks are as high as 1 in 10 may also be affected by the issues discussed in this section. What is typical is that a high proportion of the studies in the meta-analysis observe no events in one or more study arms.
10.4.4.1 Studies with no events in one or more arms
Computational problems can occur when no events are observed in one or both groups in an individual study. Inverse variance meta-analytical methods involve computing an intervention effect estimate and its standard error for each study. For studies where no events were observed in one or both arms, these computations often involve dividing by a zero count, which yields a computational error. Most meta-analytical software routines (including those in RevMan) automatically check for problematic zero counts, and add a fixed value (typically 0.5) to all cells of a 2×2 table where the problems occur. The Mantel-Haenszel methods require zero-cell corrections only if the same cell is zero in all the included studies, and hence need to use the correction less often. However, in many software applications the same correction rules are applied for Mantel-Haenszel methods as for the inverse-variance methods. Odds ratio and risk ratio methods require zero cell corrections more often than difference methods, except for the Peto odds ratio method, which encounters computation problems only in the extreme situation of no events occurring in all arms of all studies.
Whilst the fixed correction meets the objective of avoiding computational errors, it usually has the undesirable effect of biasing study estimates towards no difference and over-estimating variances of study estimates (consequently down-weighting inappropriately their contribution to the meta-analysis). Where the sizes of the study arms are unequal (which occurs more commonly in non-randomized studies than randomized trials), they will introduce a directional bias in the treatment effect. Alternative non-fixed zero-cell corrections have been explored by Sweeting and colleagues, including a correction proportional to the reciprocal of the size of the contrasting study arm, which they found preferable to the fixed 0.5 correction when arm sizes were not balanced (Sweeting et al 2004).
10.4.4.2 Studies with no events in either arm
The standard practice in meta-analysis of odds ratios and risk ratios is to exclude studies from the meta-analysis where there are no events in both arms. This is because such studies do not provide any indication of either the direction or magnitude of the relative treatment effect. Whilst it may be clear that events are very rare on both the experimental intervention and the comparator intervention, no information is provided as to which group is likely to have the higher risk, or on whether the risks are of the same or different orders of magnitude (when risks are very low, they are compatible with very large or very small ratios). Whilst one might be tempted to infer that the risk would be lowest in the group with the larger sample size (as the upper limit of the confidence interval would be lower), this is not justified as the sample size allocation was determined by the study investigators and is not a measure of the incidence of the event.
Risk difference methods superficially appear to have an advantage over odds ratio methods in that the risk difference is defined (as zero) when no events occur in either arm. Such studies are therefore included in the estimation process. Bradburn and colleagues undertook simulation studies which revealed that all risk difference methods yield confidence intervals that are too wide when events are rare, and have associated poor statistical power, which make them unsuitable for meta-analysis of rare events (Bradburn et al 2007). This is especially relevant when outcomes that focus on treatment safety are being studied, as the ability to identify correctly (or attempt to refute) serious adverse events is a key issue in drug development.
It is likely that outcomes for which no events occur in either arm may not be mentioned in reports of many randomized trials, precluding their inclusion in a meta-analysis. It is unclear, though, when working with published results, whether failure to mention a particular adverse event means there were no such events, or simply that such events were not included as a measured endpoint. Whilst the results of risk difference meta-analyses will be affected by non-reporting of outcomes with no events, odds and risk ratio based methods naturally exclude these data whether or not they are published, and are therefore unaffected.
10.4.4.3 Validity of methods of meta-analysis for rare events
Simulation studies have revealed that many meta-analytical methods can give misleading results for rare events, which is unsurprising given their reliance on asymptotic statistical theory. Their performance has been judged suboptimal either through results being biased, confidence intervals being inappropriately wide, or statistical power being too low to detect substantial differences.
In the following we consider the choice of statistical method for meta-analyses of odds ratios. Appropriate choices appear to depend on the comparator group risk, the likely size of the treatment effect and consideration of balance in the numbers of experimental and comparator participants in the constituent studies. We are not aware of research that has evaluated risk ratio measures directly, but their performance is likely to be very similar to corresponding odds ratio measurements. When events are rare, estimates of odds and risks are near identical, and results of both can be interpreted as ratios of probabilities.
Bradburn and colleagues found that many of the most commonly used meta-analytical methods were biased when events were rare (Bradburn et al 2007). The bias was greatest in inverse variance and DerSimonian and Laird odds ratio and risk difference methods, and the Mantel-Haenszel odds ratio method using a 0.5 zero-cell correction. As already noted, risk difference meta-analytical methods tended to show conservative confidence interval coverage and low statistical power when risks of events were low.
At event rates below 1% the Peto one-step odds ratio method was found to be the least biased and most powerful method, and provided the best confidence interval coverage, provided there was no substantial imbalance between treatment and comparator group sizes within studies, and treatment effects were not exceptionally large. This finding was consistently observed across three different meta-analytical scenarios, and was also observed by Sweeting and colleagues (Sweeting et al 2004).
This finding was noted despite the method producing only an approximation to the odds ratio. For very large effects (e.g. risk ratio=0.2) when the approximation is known to be poor, treatment effects were under-estimated, but the Peto method still had the best performance of all the methods considered for event risks of 1 in 1000, and the bias was never more than 6% of the comparator group risk.
In other circumstances (i.e. event risks above 1%, very large effects at event risks around 1%, and meta-analyses where many studies were substantially imbalanced) the best performing methods were the Mantel-Haenszel odds ratio without zero-cell corrections, logistic regression and an exact method. None of these methods is available in RevMan.
Methods that should be avoided with rare events are the inverse-variance methods (including the DerSimonian and Laird random-effects method) (Efthimiou 2018). These directly incorporate the study’s variance in the estimation of its contribution to the meta-analysis, but these are usually based on a large-sample variance approximation, which was not intended for use with rare events. We would suggest that incorporation of heterogeneity into an estimate of a treatment effect should be a secondary consideration when attempting to produce estimates of effects from sparse data – the primary concern is to discern whether there is any signal of an effect in the data.
10.5 Meta-analysis of continuous outcomes
An important assumption underlying standard methods for meta-analysis of continuous data is that the outcomes have a normal distribution in each intervention arm in each study. This assumption may not always be met, although it is unimportant in very large studies. It is useful to consider the possibility of skewed data (see Section 10.5.3).
10.5.1 Which effect measure for continuous outcomes?
The two summary statistics commonly used for meta-analysis of continuous data are the mean difference (MD) and the standardized mean difference (SMD). Other options are available, such as the ratio of means (see Chapter 6, Section 6.5.1). Selection of summary statistics for continuous data is principally determined by whether studies all report the outcome using the same scale (when the mean difference can be used) or using different scales (when the standardized mean difference is usually used). The ratio of means can be used in either situation, but is appropriate only when outcome measurements are strictly greater than zero. Further considerations in deciding on an effect measure that will facilitate interpretation of the findings appears in Chapter 15, Section 15.5.
The different roles played in MD and SMD approaches by the standard deviations (SDs) of outcomes observed in the two groups should be understood.
For the mean difference approach, the SDs are used together with the sample sizes to compute the weight given to each study. Studies with small SDs are given relatively higher weight whilst studies with larger SDs are given relatively smaller weights. This is appropriate if variation in SDs between studies reflects differences in the reliability of outcome measurements, but is probably not appropriate if the differences in SD reflect real differences in the variability of outcomes in the study populations.
For the standardized mean difference approach, the SDs are used to standardize the mean differences to a single scale, as well as in the computation of study weights. Thus, studies with small SDs lead to relatively higher estimates of SMD, whilst studies with larger SDs lead to relatively smaller estimates of SMD. For this to be appropriate, it must be assumed that between-study variation in SDs reflects only differences in measurement scales and not differences in the reliability of outcome measures or variability among study populations, as discussed in Chapter 6, Section 6.5.1.2.
These assumptions of the methods should be borne in mind when unexpected variation of SDs is observed across studies.
10.5.2 Meta-analysis of change scores
In some circumstances an analysis based on changes from baseline will be more efficient and powerful than comparison of post-intervention values, as it removes a component of between-person variability from the analysis. However, calculation of a change score requires measurement of the outcome twice and in practice may be less efficient for outcomes that are unstable or difficult to measure precisely, where the measurement error may be larger than true between-person baseline variability. Change-from-baseline outcomes may also be preferred if they have a less skewed distribution than post-intervention measurement outcomes. Although sometimes used as a device to ‘correct’ for unlucky randomization, this practice is not recommended.
The preferred statistical approach to accounting for baseline measurements of the outcome variable is to include the baseline outcome measurements as a covariate in a regression model or analysis of covariance (ANCOVA). These analyses produce an ‘adjusted’ estimate of the intervention effect together with its standard error. These analyses are the least frequently encountered, but as they give the most precise and least biased estimates of intervention effects they should be included in the analysis when they are available. However, they can only be included in a meta-analysis using the generic inverse-variance method, since means and SDs are not available for each intervention group separately.
In practice an author is likely to discover that the studies included in a review include a mixture of change-from-baseline and post-intervention value scores. However, mixing of outcomes is not a problem when it comes to meta-analysis of MDs. There is no statistical reason why studies with change-from-baseline outcomes should not be combined in a meta-analysis with studies with post-intervention measurement outcomes when using the (unstandardized) MD method. In a randomized study, MD based on changes from baseline can usually be assumed to be addressing exactly the same underlying intervention effects as analyses based on post-intervention measurements. That is to say, the difference in mean post-intervention values will on average be the same as the difference in mean change scores. If the use of change scores does increase precision, appropriately, the studies presenting change scores will be given higher weights in the analysis than they would have received if post-intervention values had been used, as they will have smaller SDs.
When combining the data on the MD scale, authors must be careful to use the appropriate means and SDs (either of post-intervention measurements or of changes from baseline) for each study. Since the mean values and SDs for the two types of outcome may differ substantially, it may be advisable to place them in separate subgroups to avoid confusion for the reader, but the results of the subgroups can legitimately be pooled together.
In contrast, post-intervention value and change scores should not in principle be combined using standard meta-analysis approaches when the effect measure is an SMD. This is because the SDs used in the standardization reflect different things. The SD when standardizing post-intervention values reflects between-person variability at a single point in time. The SD when standardizing change scores reflects variation in between-person changes over time, so will depend on both within-person and between-person variability; within-person variability in turn is likely to depend on the length of time between measurements. Nevertheless, an empirical study of 21 meta-analyses in osteoarthritis did not find a difference between combined SMDs based on post-intervention values and combined SMDs based on change scores (da Costa et al 2013). One option is to standardize SMDs using post-intervention SDs rather than change score SDs. This would lead to valid synthesis of the two approaches, but we are not aware that an appropriate standard error for this has been derived.
A common practical problem associated with including change-from-baseline measures is that the SD of changes is not reported. Imputation of SDs is discussed in Chapter 6, Section 6.5.2.8.
10.5.3 Meta-analysis of skewed data
Analyses based on means are appropriate for data that are at least approximately normally distributed, and for data from very large trials. If the true distribution of outcomes is asymmetrical, then the data are said to be skewed. Review authors should consider the possibility and implications of skewed data when analysing continuous outcomes (see MECIR Box 10.5.a). Skew can sometimes be diagnosed from the means and SDs of the outcomes. A rough check is available, but it is only valid if a lowest or highest possible value for an outcome is known to exist. Thus, the check may be used for outcomes such as weight, volume and blood concentrations, which have lowest possible values of 0, or for scale outcomes with minimum or maximum scores, but it may not be appropriate for change-from-baseline measures. The check involves calculating the observed mean minus the lowest possible value (or the highest possible value minus the observed mean), and dividing this by the SD. A ratio less than 2 suggests skew (Altman and Bland 1996). If the ratio is less than 1, there is strong evidence of a skewed distribution.
Transformation of the original outcome data may reduce skew substantially. Reports of trials may present results on a transformed scale, usually a log scale. Collection of appropriate data summaries from the trialists, or acquisition of individual patient data, is currently the approach of choice. Appropriate data summaries and analysis strategies for the individual patient data will depend on the situation. Consultation with a knowledgeable statistician is advised.
Where data have been analysed on a log scale, results are commonly presented as geometric means and ratios of geometric means. A meta-analysis may be then performed on the scale of the log-transformed data; an example of the calculation of the required means and SD is given in Chapter 6, Section 6.5.2.4. This approach depends on being able to obtain transformed data for all studies; methods for transforming from one scale to the other are available (Higgins et al 2008b). Log-transformed and untransformed data should not be mixed in a meta-analysis.
MECIR Box 10.5.a Relevant expectations for conduct of intervention reviews
|
C65: Addressing skewed data (Highly desirable) |
|
|
Consider the possibility and implications of skewed data when analysing continuous outcomes. |
Skewed data are sometimes not summarized usefully by means and standard deviations. While statistical methods are approximately valid for large sample sizes, skewed outcome data can lead to misleading results when studies are small. |
10.6 Combining dichotomous and continuous outcomes
Occasionally authors encounter a situation where data for the same outcome are presented in some studies as dichotomous data and in other studies as continuous data. For example, scores on depression scales can be reported as means, or as the percentage of patients who were depressed at some point after an intervention (i.e. with a score above a specified cut-point). This type of information is often easier to understand, and more helpful, when it is dichotomized. However, deciding on a cut-point may be arbitrary, and information is lost when continuous data are transformed to dichotomous data.
There are several options for handling combinations of dichotomous and continuous data. Generally, it is useful to summarize results from all the relevant, valid studies in a similar way, but this is not always possible. It may be possible to collect missing data from investigators so that this can be done. If not, it may be useful to summarize the data in three ways: by entering the means and SDs as continuous outcomes, by entering the counts as dichotomous outcomes and by entering all of the data in text form as ‘Other data’ outcomes.
There are statistical approaches available that will re-express odds ratios as SMDs (and vice versa), allowing dichotomous and continuous data to be combined (Anzures-Cabrera et al 2011). A simple approach is as follows. Based on an assumption that the underlying continuous measurements in each intervention group follow a logistic distribution (which is a symmetrical distribution similar in shape to the normal distribution, but with more data in the distributional tails), and that the variability of the outcomes is the same in both experimental and comparator participants, the odds ratios can be re-expressed as a SMD according to the following simple formula (Chinn 2000):
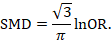
The standard error of the log odds ratio can be converted to the standard error of a SMD by multiplying by the same constant (√3/π=0.5513). Alternatively SMDs can be re-expressed as log odds ratios by multiplying by π/√3=1.814. Once SMDs (or log odds ratios) and their standard errors have been computed for all studies in the meta-analysis, they can be combined using the generic inverse-variance method. Standard errors can be computed for all studies by entering the data as dichotomous and continuous outcome type data, as appropriate, and converting the confidence intervals for the resulting log odds ratios and SMDs into standard errors (see Chapter 6, Section 6.3).
10.7 Meta-analysis of ordinal outcomes and measurement scales
Ordinal and measurement scale outcomes are most commonly meta-analysed as dichotomous data (if so, see Section 10.4) or continuous data (if so, see Section 10.5) depending on the way that the study authors performed the original analyses.
Occasionally it is possible to analyse the data using proportional odds models. This is the case when ordinal scales have a small number of categories, the numbers falling into each category for each intervention group can be obtained, and the same ordinal scale has been used in all studies. This approach may make more efficient use of all available data than dichotomization, but requires access to statistical software and results in a summary statistic for which it is challenging to find a clinical meaning.
The proportional odds model uses the proportional odds ratio as the measure of intervention effect (Agresti 1996) (see Chapter 6, Section 6.6), and can be used for conducting a meta-analysis in advanced statistical software packages (Whitehead and Jones 1994). Estimates of log odds ratios and their standard errors from a proportional odds model may be meta-analysed using the generic inverse-variance method (see Section 10.3.3). If the same ordinal scale has been used in all studies, but in some reports has been presented as a dichotomous outcome, it may still be possible to include all studies in the meta-analysis. In the context of the three-category model, this might mean that for some studies category 1 constitutes a success, while for others both categories 1 and 2 constitute a success. Methods are available for dealing with this, and for combining data from scales that are related but have different definitions for their categories (Whitehead and Jones 1994).
10.8 Meta-analysis of counts and rates
Results may be expressed as count data when each participant may experience an event, and may experience it more than once (see Chapter 6, Section 6.7). For example, ‘number of strokes’, or ‘number of hospital visits’ are counts. These events may not happen at all, but if they do happen there is no theoretical maximum number of occurrences for an individual. Count data may be analysed using methods for dichotomous data if the counts are dichotomized for each individual (see Section 10.4), continuous data (see Section 10.5) and time-to-event data (see Section 10.9), as well as being analysed as rate data.
Rate data occur if counts are measured for each participant along with the time over which they are observed. This is particularly appropriate when the events being counted are rare. For example, a woman may experience two strokes during a follow-up period of two years. Her rate of strokes is one per year of follow-up (or, equivalently 0.083 per month of follow-up). Rates are conventionally summarized at the group level. For example, participants in the comparator group of a clinical trial may experience 85 strokes during a total of 2836 person-years of follow-up. An underlying assumption associated with the use of rates is that the risk of an event is constant across participants and over time. This assumption should be carefully considered for each situation. For example, in contraception studies, rates have been used (known as Pearl indices) to describe the number of pregnancies per 100 women-years of follow-up. This is now considered inappropriate since couples have different risks of conception, and the risk for each woman changes over time. Pregnancies are now analysed more often using life tables or time-to-event methods that investigate the time elapsing before the first pregnancy.
Analysing count data as rates is not always the most appropriate approach and is uncommon in practice. This is because:
- the assumption of a constant underlying risk may not be suitable; and
- the statistical methods are not as well developed as they are for other types of data.
The results of a study may be expressed as a rate ratio, that is the ratio of the rate in the experimental intervention group to the rate in the comparator group. The (natural) logarithms of the rate ratios may be combined across studies using the generic inverse-variance method (see Section 10.3.3). Alternatively, Poisson regression approaches can be used (Spittal et al 2015).
In a randomized trial, rate ratios may often be very similar to risk ratios obtained after dichotomizing the participants, since the average period of follow-up should be similar in all intervention groups. Rate ratios and risk ratios will differ, however, if an intervention affects the likelihood of some participants experiencing multiple events.
It is possible also to focus attention on the rate difference (see Chapter 6, Section 6.7.1). The analysis again can be performed using the generic inverse-variance method (Hasselblad and McCrory 1995, Guevara et al 2004).
10.9 Meta-analysis of time-to-event outcomes
Two approaches to meta-analysis of time-to-event outcomes are readily available to Cochrane Review authors. The choice of which to use will depend on the type of data that have been extracted from the primary studies, or obtained from re-analysis of individual participant data.
If ‘O – E’ and ‘V’ statistics have been obtained (see Chapter 6, Section 6.8.2), either through re-analysis of individual participant data or from aggregate statistics presented in the study reports, then these statistics may be entered directly into RevMan using the ‘O – E and Variance’ outcome type. There are several ways to calculate these ‘O – E’ and ‘V’ statistics. Peto’s method applied to dichotomous data (Section 10.4.2) gives rise to an odds ratio; a log-rank approach gives rise to a hazard ratio; and a variation of the Peto method for analysing time-to-event data gives rise to something in between (Simmonds et al 2011). The appropriate effect measure should be specified. Only fixed-effect meta-analysis methods are available in RevMan for ‘O – E and Variance’ outcomes.
Alternatively, if estimates of log hazard ratios and standard errors have been obtained from results of Cox proportional hazards regression models, study results can be combined using generic inverse-variance methods (see Section 10.3.3).
If a mixture of log-rank and Cox model estimates are obtained from the studies, all results can be combined using the generic inverse-variance method, as the log-rank estimates can be converted into log hazard ratios and standard errors using the approaches discussed in Chapter 6, Section 6.8.
10.10 Heterogeneity
10.10.1 What is heterogeneity?
Inevitably, studies brought together in a systematic review will differ. Any kind of variability among studies in a systematic review may be termed heterogeneity. It can be helpful to distinguish between different types of heterogeneity. Variability in the participants, interventions and outcomes studied may be described as clinical diversity (sometimes called clinical heterogeneity), and variability in study design, outcome measurement tools and risk of bias may be described as methodological diversity (sometimes called methodological heterogeneity). Variability in the intervention effects being evaluated in the different studies is known as statistical heterogeneity, and is a consequence of clinical or methodological diversity, or both, among the studies. Statistical heterogeneity manifests itself in the observed intervention effects being more different from each other than one would expect due to random error (chance) alone. We will follow convention and refer to statistical heterogeneity simply as heterogeneity.
Clinical variation will lead to heterogeneity if the intervention effect is affected by the factors that vary across studies; most obviously, the specific interventions or patient characteristics. In other words, the true intervention effect will be different in different studies.
Differences between studies in terms of methodological factors, such as use of blinding and concealment of allocation sequence, or if there are differences between studies in the way the outcomes are defined and measured, may be expected to lead to differences in the observed intervention effects. Significant statistical heterogeneity arising from methodological diversity or differences in outcome assessments suggests that the studies are not all estimating the same quantity, but does not necessarily suggest that the true intervention effect varies. In particular, heterogeneity associated solely with methodological diversity would indicate that the studies suffer from different degrees of bias. Empirical evidence suggests that some aspects of design can affect the result of clinical trials, although this is not always the case. Further discussion appears in Chapter 7 and Chapter 8.
The scope of a review will largely determine the extent to which studies included in a review are diverse. Sometimes a review will include studies addressing a variety of questions, for example when several different interventions for the same condition are of interest (see also Chapter 11) or when the differential effects of an intervention in different populations are of interest. Meta-analysis should only be considered when a group of studies is sufficiently homogeneous in terms of participants, interventions and outcomes to provide a meaningful summary. It is often appropriate to take a broader perspective in a meta-analysis than in a single clinical trial. A common analogy is that systematic reviews bring together apples and oranges, and that combining these can yield a meaningless result. This is true if apples and oranges are of intrinsic interest on their own, but may not be if they are used to contribute to a wider question about fruit. For example, a meta-analysis may reasonably evaluate the average effect of a class of drugs by combining results from trials where each evaluates the effect of a different drug from the class.
There may be specific interest in a review in investigating how clinical and methodological aspects of studies relate to their results. Where possible these investigations should be specified a priori (i.e. in the protocol for the systematic review). It is legitimate for a systematic review to focus on examining the relationship between some clinical characteristic(s) of the studies and the size of intervention effect, rather than on obtaining a summary effect estimate across a series of studies (see Section 10.11). Meta-regression may best be used for this purpose, although it is not implemented in RevMan (see Section 10.11.4).
10.10.2 Identifying and measuring heterogeneity
It is essential to consider the extent to which the results of studies are consistent with each other (see MECIR Box 10.10.a). If confidence intervals for the results of individual studies (generally depicted graphically using horizontal lines) have poor overlap, this generally indicates the presence of statistical heterogeneity. More formally, a statistical test for heterogeneity is available. This Chi2 (χ2, or chi-squared) test is included in the forest plots in Cochrane Reviews. It assesses whether observed differences in results are compatible with chance alone. A low P value (or a large Chi2 statistic relative to its degree of freedom) provides evidence of heterogeneity of intervention effects (variation in effect estimates beyond chance).
MECIR Box 10.10.a Relevant expectations for conduct of intervention reviews
|
C63: Assessing statistical heterogeneity (Mandatory) |
|
|
Assess the presence and extent of between-study variation when undertaking a meta-analysis. |
The presence of heterogeneity affects the extent to which generalizable conclusions can be formed. It is important to identify heterogeneity in case there is sufficient information to explain it and offer new insights. Authors should recognize that there is much uncertainty in measures such as I2 and Tau2 when there are few studies. Thus, use of simple thresholds to diagnose heterogeneity should be avoided. |
Care must be taken in the interpretation of the Chi2 test, since it has low power in the (common) situation of a meta-analysis when studies have small sample size or are few in number. This means that while a statistically significant result may indicate a problem with heterogeneity, a non-significant result must not be taken as evidence of no heterogeneity. This is also why a P value of 0.10, rather than the conventional level of 0.05, is sometimes used to determine statistical significance. A further problem with the test, which seldom occurs in Cochrane Reviews, is that when there are many studies in a meta-analysis, the test has high power to detect a small amount of heterogeneity that may be clinically unimportant.
Some argue that, since clinical and methodological diversity always occur in a meta-analysis, statistical heterogeneity is inevitable (Higgins et al 2003). Thus, the test for heterogeneity is irrelevant to the choice of analysis; heterogeneity will always exist whether or not we happen to be able to detect it using a statistical test. Methods have been developed for quantifying inconsistency across studies that move the focus away from testing whether heterogeneity is present to assessing its impact on the meta-analysis. A useful statistic for quantifying inconsistency is:
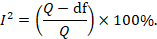
In this equation, Q is the Chi2 statistic and df is its degrees of freedom (Higgins and Thompson 2002, Higgins et al 2003). I2 describes the percentage of the variability in effect estimates that is due to heterogeneity rather than sampling error (chance).
Thresholds for the interpretation of the I2 statistic can be misleading, since the importance of inconsistency depends on several factors. A rough guide to interpretation in the context of meta-analyses of randomized trials is as follows:
- 0% to 40%: might not be important;
- 30% to 60%: may represent moderate heterogeneity*;
- 50% to 90%: may represent substantial heterogeneity*;
- 75% to 100%: considerable heterogeneity*.
*The importance of the observed value of I2 depends on (1) magnitude and direction of effects, and (2) strength of evidence for heterogeneity (e.g. P value from the Chi2 test, or a confidence interval for I2: uncertainty in the value of I2 is substantial when the number of studies is small).
10.10.3 Strategies for addressing heterogeneity
Review authors must take into account any statistical heterogeneity when interpreting results, particularly when there is variation in the direction of effect (see MECIR Box 10.10.b). A number of options are available if heterogeneity is identified among a group of studies that would otherwise be considered suitable for a meta-analysis.
MECIR Box 10.10.b Relevant expectations for conduct of intervention reviews
|
C69: Considering statistical heterogeneity when interpreting the results (Mandatory) |
|
|
Take into account any statistical heterogeneity when interpreting the results, particularly when there is variation in the direction of effect. |
The presence of heterogeneity affects the extent to which generalizable conclusions can be formed. If a fixed-effect analysis is used, the confidence intervals ignore the extent of heterogeneity. If a random-effects analysis is used, the result pertains to the mean effect across studies. In both cases, the implications of notable heterogeneity should be addressed. It may be possible to understand the reasons for the heterogeneity if there are sufficient studies. |
-
Check again that the data are correct. Severe apparent heterogeneity can indicate that data have been incorrectly extracted or entered into meta-analysis software. For example, if standard errors have mistakenly been entered as SDs for continuous outcomes, this could manifest itself in overly narrow confidence intervals with poor overlap and hence substantial heterogeneity. Unit-of-analysis errors may also be causes of heterogeneity (see Chapter 6, Section 6.2).
-
Do not do a meta-analysis. A systematic review need not contain any meta-analyses. If there is considerable variation in results, and particularly if there is inconsistency in the direction of effect, it may be misleading to quote an average value for the intervention effect.
-
Explore heterogeneity. It is clearly of interest to determine the causes of heterogeneity among results of studies. This process is problematic since there are often many characteristics that vary across studies from which one may choose. Heterogeneity may be explored by conducting subgroup analyses (see Section 10.11.3) or meta-regression (see Section 10.11.4). Reliable conclusions can only be drawn from analyses that are truly pre-specified before inspecting the studies’ results, and even these conclusions should be interpreted with caution. Explorations of heterogeneity that are devised after heterogeneity is identified can at best lead to the generation of hypotheses. They should be interpreted with even more caution and should generally not be listed among the conclusions of a review. Also, investigations of heterogeneity when there are very few studies are of questionable value.
-
Ignore heterogeneity. Fixed-effect meta-analyses ignore heterogeneity. The summary effect estimate from a fixed-effect meta-analysis is normally interpreted as being the best estimate of the intervention effect. However, the existence of heterogeneity suggests that there may not be a single intervention effect but a variety of intervention effects. Thus, the summary fixed-effect estimate may be an intervention effect that does not actually exist in any population, and therefore have a confidence interval that is meaningless as well as being too narrow (see Section 10.10.4).
-
Perform a random-effects meta-analysis. A random-effects meta-analysis may be used to incorporate heterogeneity among studies. This is not a substitute for a thorough investigation of heterogeneity. It is intended primarily for heterogeneity that cannot be explained. An extended discussion of this option appears in Section 10.10.4.
-
Reconsider the effect measure. Heterogeneity may be an artificial consequence of an inappropriate choice of effect measure. For example, when studies collect continuous outcome data using different scales or different units, extreme heterogeneity may be apparent when using the mean difference but not when the more appropriate standardized mean difference is used. Furthermore, choice of effect measure for dichotomous outcomes (odds ratio, risk ratio, or risk difference) may affect the degree of heterogeneity among results. In particular, when comparator group risks vary, homogeneous odds ratios or risk ratios will necessarily lead to heterogeneous risk differences, and vice versa. However, it remains unclear whether homogeneity of intervention effect in a particular meta-analysis is a suitable criterion for choosing between these measures (see also Section 10.4.3).
- Exclude studies. Heterogeneity may be due to the presence of one or two outlying studies with results that conflict with the rest of the studies. In general it is unwise to exclude studies from a meta-analysis on the basis of their results as this may introduce bias. However, if an obvious reason for the outlying result is apparent, the study might be removed with more confidence. Since usually at least one characteristic can be found for any study in any meta-analysis which makes it different from the others, this criterion is unreliable because it is all too easy to fulfil. It is advisable to perform analyses both with and without outlying studies as part of a sensitivity analysis (see Section 10.14). Whenever possible, potential sources of clinical diversity that might lead to such situations should be specified in the protocol.
10.10.4 Incorporating heterogeneity into random-effects models
The random-effects meta-analysis approach incorporates an assumption that the different studies are estimating different, yet related, intervention effects (DerSimonian and Laird 1986, Borenstein et al 2010). The approach allows us to address heterogeneity that cannot readily be explained by other factors. A random-effects meta-analysis model involves an assumption that the effects being estimated in the different studies follow some distribution. The model represents our lack of knowledge about why real, or apparent, intervention effects differ, by considering the differences as if they were random. The centre of the assumed distribution describes the average of the effects, while its width describes the degree of heterogeneity. The conventional choice of distribution is a normal distribution. It is difficult to establish the validity of any particular distributional assumption, and this is a common criticism of random-effects meta-analyses. The importance of the assumed shape for this distribution has not been widely studied.
To undertake a random-effects meta-analysis, the standard errors of the study-specific estimates (SEi in Section 10.3.1) are adjusted to incorporate a measure of the extent of variation, or heterogeneity, among the intervention effects observed in different studies (this variation is often referred to as Tau-squared, τ2, or Tau2). The amount of variation, and hence the adjustment, can be estimated from the intervention effects and standard errors of the studies included in the meta-analysis.
In a heterogeneous set of studies, a random-effects meta-analysis will award relatively more weight to smaller studies than such studies would receive in a fixed-effect meta-analysis. This is because small studies are more informative for learning about the distribution of effects across studies than for learning about an assumed common intervention effect.
Note that a random-effects model does not ‘take account’ of the heterogeneity, in the sense that it is no longer an issue. It is always preferable to explore possible causes of heterogeneity, although there may be too few studies to do this adequately (see Section 10.11).
10.10.4.1 Fixed or random effects?
A fixed-effect meta-analysis provides a result that may be viewed as a ‘typical intervention effect’ from the studies included in the analysis. In order to calculate a confidence interval for a fixed-effect meta-analysis the assumption is usually made that the true effect of intervention (in both magnitude and direction) is the same value in every study (i.e. fixed across studies). This assumption implies that the observed differences among study results are due solely to the play of chance (i.e. that there is no statistical heterogeneity).
A random-effects model provides a result that may be viewed as an ‘average intervention effect’, where this average is explicitly defined according to an assumed distribution of effects across studies. Instead of assuming that the intervention effects are the same, we assume that they follow (usually) a normal distribution. The assumption implies that the observed differences among study results are due to a combination of the play of chance and some genuine variation in the intervention effects.
The random-effects method and the fixed-effect method will give identical results when there is no heterogeneity among the studies.
When heterogeneity is present, a confidence interval around the random-effects summary estimate is wider than a confidence interval around a fixed-effect summary estimate. This will happen whenever the I2 statistic is greater than zero, even if the heterogeneity is not detected by the Chi2 test for heterogeneity (see Section 10.10.2).
Sometimes the central estimate of the intervention effect is different between fixed-effect and random-effects analyses. In particular, if results of smaller studies are systematically different from results of larger ones, which can happen as a result of publication bias or within-study bias in smaller studies (Egger et al 1997, Poole and Greenland 1999, Kjaergard et al 2001), then a random-effects meta-analysis will exacerbate the effects of the bias (see also Chapter 13, Section 13.3.5.6). A fixed-effect analysis will be affected less, although strictly it will also be inappropriate.
The decision between fixed- and random-effects meta-analyses has been the subject of much debate, and we do not provide a universal recommendation. Some considerations in making this choice are as follows:
- Many have argued that the decision should be based on an expectation of whether the intervention effects are truly identical, preferring the fixed-effect model if this is likely and a random-effects model if this is unlikely (Borenstein et al 2010). Since it is generally considered to be implausible that intervention effects across studies are identical (unless the intervention has no effect at all), this leads many to advocate use of the random-effects model.
- Others have argued that a fixed-effect analysis can be interpreted in the presence of heterogeneity, and that it makes fewer assumptions than a random-effects meta-analysis. They then refer to it as a ‘fixed-effects’ meta-analysis (Peto et al 1995, Rice et al 2018).
- Under any interpretation, a fixed-effect meta-analysis ignores heterogeneity. If the method is used, it is therefore important to supplement it with a statistical investigation of the extent of heterogeneity (see Section 10.10.2).
- In the presence of heterogeneity, a random-effects analysis gives relatively more weight to smaller studies and relatively less weight to larger studies. If there is additionally some funnel plot asymmetry (i.e. a relationship between intervention effect magnitude and study size), then this will push the results of the random-effects analysis towards the findings in the smaller studies. In the context of randomized trials, this is generally regarded as an unfortunate consequence of the model.
- A pragmatic approach is to plan to undertake both a fixed-effect and a random-effects meta-analysis, with an intention to present the random-effects result if there is no indication of funnel plot asymmetry. If there is an indication of funnel plot asymmetry, then both methods are problematic. It may be reasonable to present both analyses or neither, or to perform a sensitivity analysis in which small studies are excluded or addressed directly using meta-regression (see Chapter 13, Section 13.3.5.6).
- The choice between a fixed-effect and a random-effects meta-analysis should never be made on the basis of a statistical test for heterogeneity.
10.10.4.2 Interpretation of random-effects meta-analyses
The summary estimate and confidence interval from a random-effects meta-analysis refer to the centre of the distribution of intervention effects, but do not describe the width of the distribution. Often the summary estimate and its confidence interval are quoted in isolation and portrayed as a sufficient summary of the meta-analysis. This is inappropriate. The confidence interval from a random-effects meta-analysis describes uncertainty in the location of the mean of systematically different effects in the different studies. It does not describe the degree of heterogeneity among studies, as may be commonly believed. For example, when there are many studies in a meta-analysis, we may obtain a very tight confidence interval around the random-effects estimate of the mean effect even when there is a large amount of heterogeneity. A solution to this problem is to consider a prediction interval (see Section 10.10.4.3).
Methodological diversity creates heterogeneity through biases variably affecting the results of different studies. The random-effects summary estimate will only correctly estimate the average intervention effect if the biases are symmetrically distributed, leading to a mixture of over-estimates and under-estimates of effect, which is unlikely to be the case. In practice it can be very difficult to distinguish whether heterogeneity results from clinical or methodological diversity, and in most cases it is likely to be due to both, so these distinctions are hard to draw in the interpretation.
When there is little information, either because there are few studies or if the studies are small with few events, a random-effects analysis will provide poor estimates of the amount of heterogeneity (i.e. of the width of the distribution of intervention effects). Fixed-effect methods such as the Mantel-Haenszel method will provide more robust estimates of the average intervention effect, but at the cost of ignoring any heterogeneity.
10.10.4.3 Prediction intervals from a random-effects meta-analysis
An estimate of the between-study variance in a random-effects meta-analysis is typically presented as part of its results. The square root of this number (i.e. Tau) is the estimated standard deviation of underlying effects across studies. Prediction intervals are a way of expressing this value in an interpretable way.
To motivate the idea of a prediction interval, note that for absolute measures of effect (e.g. risk difference, mean difference, standardized mean difference), an approximate 95% range of normally distributed underlying effects can be obtained by creating an interval from 1.96´Tau below the random-effects mean, to 1.96✕Tau above it. (For relative measures such as the odds ratio and risk ratio, an equivalent interval needs to be based on the natural logarithm of the summary estimate.) In reality, both the summary estimate and the value of Tau are associated with uncertainty. A prediction interval seeks to present the range of effects in a way that acknowledges this uncertainty (Higgins et al 2009). A simple 95% prediction interval can be calculated as:
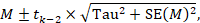
where M is the summary mean from the random-effects meta-analysis, tk−2 is the 95% percentile of a t-distribution with k–2 degrees of freedom, k is the number of studies, Tau2 is the estimated amount of heterogeneity and SE(M) is the standard error of the summary mean.
The term ‘prediction interval’ relates to the use of this interval to predict the possible underlying effect in a new study that is similar to the studies in the meta-analysis. A more useful interpretation of the interval is as a summary of the spread of underlying effects in the studies included in the random-effects meta-analysis.
Prediction intervals have proved a popular way of expressing the amount of heterogeneity in a meta-analysis (Riley et al 2011). They are, however, strongly based on the assumption of a normal distribution for the effects across studies, and can be very problematic when the number of studies is small, in which case they can appear spuriously wide or spuriously narrow. Nevertheless, we encourage their use when the number of studies is reasonable (e.g. more than ten) and there is no clear funnel plot asymmetry.
10.10.4.4 Implementing random-effects meta-analyses
As introduced in Section 10.3.2, the random-effects model can be implemented using an inverse-variance approach, incorporating a measure of the extent of heterogeneity into the study weights. RevMan implements a version of random-effects meta-analysis that is described by DerSimonian and Laird, making use of a ‘moment-based’ estimate of the between-study variance (DerSimonian and Laird 1986). The attraction of this method is that the calculations are straightforward, but it has a theoretical disadvantage in that the confidence intervals are slightly too narrow to encompass full uncertainty resulting from having estimated the degree of heterogeneity.
For many years, RevMan has implemented two random-effects methods for dichotomous data: a Mantel-Haenszel method and an inverse-variance method. Both use the moment-based approach to estimating the amount of between-studies variation. The difference between the two is subtle: the former estimates the between-study variation by comparing each study’s result with a Mantel-Haenszel fixed-effect meta-analysis result, whereas the latter estimates it by comparing each study’s result with an inverse-variance fixed-effect meta-analysis result. In practice, the difference is likely to be trivial.
There are alternative methods for performing random-effects meta-analyses that have better technical properties than the DerSimonian and Laird approach with a moment-based estimate (Veroniki et al 2016). Most notable among these is an adjustment to the confidence interval proposed by Hartung and Knapp and by Sidik and Jonkman (Hartung and Knapp 2001, Sidik and Jonkman 2002). This adjustment widens the confidence interval to reflect uncertainty in the estimation of between-study heterogeneity, and it should be used if available to review authors. An alternative option to encompass full uncertainty in the degree of heterogeneity is to take a Bayesian approach (see Section 10.13).
An empirical comparison of different ways to estimate between-study variation in Cochrane meta-analyses has shown that they can lead to substantial differences in estimates of heterogeneity, but seldom have major implications for estimating summary effects (Langan et al 2015). Several simulation studies have concluded that an approach proposed by Paule and Mandel should be recommended (Langan et al 2017); whereas a comprehensive recent simulation study recommended a restricted maximum likelihood approach, although noted that no single approach is universally preferable (Langan et al 2019). Review authors are encouraged to select one of these options if it is available to them.
10.11 Investigating heterogeneity
10.11.1 Interaction and effect modification
Does the intervention effect vary with different populations or intervention characteristics (such as dose or duration)? Such variation is known as interaction by statisticians and as effect modification by epidemiologists. Methods to search for such interactions include subgroup analyses and meta-regression. All methods have considerable pitfalls.
10.11.2 What are subgroup analyses?
Subgroup analyses involve splitting all the participant data into subgroups, often in order to make comparisons between them. Subgroup analyses may be done for subsets of participants (such as males and females), or for subsets of studies (such as different geographical locations). Subgroup analyses may be done as a means of investigating heterogeneous results, or to answer specific questions about particular patient groups, types of intervention or types of study.
Subgroup analyses of subsets of participants within studies are uncommon in systematic reviews based on published literature because sufficient details to extract data about separate participant types are seldom published in reports. By contrast, such subsets of participants are easily analysed when individual participant data have been collected (see Chapter 26). The methods we describe in the remainder of this chapter are for subgroups of studies.
Findings from multiple subgroup analyses may be misleading. Subgroup analyses are observational by nature and are not based on randomized comparisons. False negative and false positive significance tests increase in likelihood rapidly as more subgroup analyses are performed. If their findings are presented as definitive conclusions there is clearly a risk of people being denied an effective intervention or treated with an ineffective (or even harmful) intervention. Subgroup analyses can also generate misleading recommendations about directions for future research that, if followed, would waste scarce resources.
It is useful to distinguish between the notions of ‘qualitative interaction’ and ‘quantitative interaction’ (Yusuf et al 1991). Qualitative interaction exists if the direction of effect is reversed, that is if an intervention is beneficial in one subgroup but is harmful in another. Qualitative interaction is rare. This may be used as an argument that the most appropriate result of a meta-analysis is the overall effect across all subgroups. Quantitative interaction exists when the size of the effect varies but not the direction, that is if an intervention is beneficial to different degrees in different subgroups.
10.11.3 Undertaking subgroup analyses
Meta-analyses can be undertaken in RevMan both within subgroups of studies as well as across all studies irrespective of their subgroup membership. It is tempting to compare effect estimates in different subgroups by considering the meta-analysis results from each subgroup separately. This should only be done informally by comparing the magnitudes of effect. Noting that either the effect or the test for heterogeneity in one subgroup is statistically significant whilst that in the other subgroup is not statistically significant does not indicate that the subgroup factor explains heterogeneity. Since different subgroups are likely to contain different amounts of information and thus have different abilities to detect effects, it is extremely misleading simply to compare the statistical significance of the results.
10.11.3.1 Is the effect different in different subgroups?
Valid investigations of whether an intervention works differently in different subgroups involve comparing the subgroups with each other. It is a mistake to compare within-subgroup inferences such as P values. If one subgroup analysis is statistically significant and another is not, then the latter may simply reflect a lack of information rather than a smaller (or absent) effect. When there are only two subgroups, non-overlap of the confidence intervals indicates statistical significance, but note that the confidence intervals can overlap to a small degree and the difference still be statistically significant.
A formal statistical approach should be used to examine differences among subgroups (see MECIR Box 10.11.a). A simple significance test to investigate differences between two or more subgroups can be performed (Borenstein and Higgins 2013). This procedure consists of undertaking a standard test for heterogeneity across subgroup results rather than across individual study results. When the meta-analysis uses a fixed-effect inverse-variance weighted average approach, the method is exactly equivalent to the test described by Deeks and colleagues (Deeks et al 2001). An I2 statistic is also computed for subgroup differences. This describes the percentage of the variability in effect estimates from the different subgroups that is due to genuine subgroup differences rather than sampling error (chance). Note that these methods for examining subgroup differences should be used only when the data in the subgroups are independent (i.e. they should not be used if the same study participants contribute to more than one of the subgroups in the forest plot).
If fixed-effect models are used for the analysis within each subgroup, then these statistics relate to differences in typical effects across different subgroups. If random-effects models are used for the analysis within each subgroup, then the statistics relate to variation in the mean effects in the different subgroups.
An alternative method for testing for differences between subgroups is to use meta-regression techniques, in which case a random-effects model is generally preferred (see Section 10.11.4). Tests for subgroup differences based on random-effects models may be regarded as preferable to those based on fixed-effect models, due to the high risk of false-positive results when a fixed-effect model is used to compare subgroups (Higgins and Thompson 2004).
MECIR Box 10.11.a Relevant expectations for conduct of intervention reviews
|
C67: Comparing subgroups (Mandatory) |
|
|
If subgroup analyses are to be compared, and there are judged to be sufficient studies to do this meaningfully, use a formal statistical test to compare them. |
Concluding that there is a difference in effect in different subgroups on the basis of differences in the level of statistical significance within subgroups can be very misleading. |
10.11.4 Meta-regression
If studies are divided into subgroups (see Section 10.11.2), this may be viewed as an investigation of how a categorical study characteristic is associated with the intervention effects in the meta-analysis. For example, studies in which allocation sequence concealment was adequate may yield different results from those in which it was inadequate. Here, allocation sequence concealment, being either adequate or inadequate, is a categorical characteristic at the study level. Meta-regression is an extension to subgroup analyses that allows the effect of continuous, as well as categorical, characteristics to be investigated, and in principle allows the effects of multiple factors to be investigated simultaneously (although this is rarely possible due to inadequate numbers of studies) (Thompson and Higgins 2002). Meta-regression should generally not be considered when there are fewer than ten studies in a meta-analysis.
Meta-regressions are similar in essence to simple regressions, in which an outcome variable is predicted according to the values of one or more explanatory variables. In meta-regression, the outcome variable is the effect estimate (for example, a mean difference, a risk difference, a log odds ratio or a log risk ratio). The explanatory variables are characteristics of studies that might influence the size of intervention effect. These are often called ‘potential effect modifiers’ or covariates. Meta-regressions usually differ from simple regressions in two ways. First, larger studies have more influence on the relationship than smaller studies, since studies are weighted by the precision of their respective effect estimate. Second, it is wise to allow for the residual heterogeneity among intervention effects not modelled by the explanatory variables. This gives rise to the term ‘random-effects meta-regression’, since the extra variability is incorporated in the same way as in a random-effects meta-analysis (Thompson and Sharp 1999).
The regression coefficient obtained from a meta-regression analysis will describe how the outcome variable (the intervention effect) changes with a unit increase in the explanatory variable (the potential effect modifier). The statistical significance of the regression coefficient is a test of whether there is a linear relationship between intervention effect and the explanatory variable. If the intervention effect is a ratio measure, the log-transformed value of the intervention effect should always be used in the regression model (see Chapter 6, Section 6.1.2.1), and the exponential of the regression coefficient will give an estimate of the relative change in intervention effect with a unit increase in the explanatory variable.
Meta-regression can also be used to investigate differences for categorical explanatory variables as done in subgroup analyses. If there are J subgroups, membership of particular subgroups is indicated by using J minus 1 dummy variables (which can only take values of zero or one) in the meta-regression model (as in standard linear regression modelling). The regression coefficients will estimate how the intervention effect in each subgroup differs from a nominated reference subgroup. The P value of each regression coefficient will indicate the strength of evidence against the null hypothesis that the characteristic is not associated with the intervention effect.
Meta-regression may be performed using the ‘metareg’ macro available for the Stata statistical package, or using the ‘metafor’ package for R, as well as other packages.
10.11.5 Selection of study characteristics for subgroup analyses and meta-regression
Authors need to be cautious about undertaking subgroup analyses, and interpreting any that they do. Some considerations are outlined here for selecting characteristics (also called explanatory variables, potential effect modifiers or covariates) that will be investigated for their possible influence on the size of the intervention effect. These considerations apply similarly to subgroup analyses and to meta-regressions. Further details may be obtained elsewhere (Oxman and Guyatt 1992, Berlin and Antman 1994).
10.11.5.1 Ensure that there are adequate studies to justify subgroup analyses and meta-regressions
It is very unlikely that an investigation of heterogeneity will produce useful findings unless there is a substantial number of studies. Typical advice for undertaking simple regression analyses: that at least ten observations (i.e. ten studies in a meta-analysis) should be available for each characteristic modelled. However, even this will be too few when the covariates are unevenly distributed across studies.
10.11.5.2 Specify characteristics in advance
Authors should, whenever possible, pre-specify characteristics in the protocol that later will be subject to subgroup analyses or meta-regression. The plan specified in the protocol should then be followed (data permitting), without undue emphasis on any particular findings (see MECIR Box 10.11.b). Pre-specifying characteristics reduces the likelihood of spurious findings, first by limiting the number of subgroups investigated, and second by preventing knowledge of the studies’ results influencing which subgroups are analysed. True pre-specification is difficult in systematic reviews, because the results of some of the relevant studies are often known when the protocol is drafted. If a characteristic was overlooked in the protocol, but is clearly of major importance and justified by external evidence, then authors should not be reluctant to explore it. However, such post-hoc analyses should be identified as such.
MECIR Box 10.11.b Relevant expectations for conduct of intervention reviews
|
C68: Interpreting subgroup analyses (Mandatory) |
|
|
If subgroup analyses are conducted, follow the subgroup analysis plan specified in the protocol without undue emphasis on particular findings. |
Selective reporting, or over-interpretation, of particular subgroups or particular subgroup analyses should be avoided. This is a problem especially when multiple subgroup analyses are performed. This does not preclude the use of sensible and honest post hoc subgroup analyses. |
10.11.5.3 Select a small number of characteristics
The likelihood of a false-positive result among subgroup analyses and meta-regression increases with the number of characteristics investigated. It is difficult to suggest a maximum number of characteristics to look at, especially since the number of available studies is unknown in advance. If more than one or two characteristics are investigated it may be sensible to adjust the level of significance to account for making multiple comparisons.
10.11.5.4 Ensure there is scientific rationale for investigating each characteristic
Selection of characteristics should be motivated by biological and clinical hypotheses, ideally supported by evidence from sources other than the included studies. Subgroup analyses using characteristics that are implausible or clinically irrelevant are not likely to be useful and should be avoided. For example, a relationship between intervention effect and year of publication is seldom in itself clinically informative, and if identified runs the risk of initiating a post-hoc data dredge of factors that may have changed over time.
Prognostic factors are those that predict the outcome of a disease or condition, whereas effect modifiers are factors that influence how well an intervention works in affecting the outcome. Confusion between prognostic factors and effect modifiers is common in planning subgroup analyses, especially at the protocol stage. Prognostic factors are not good candidates for subgroup analyses unless they are also believed to modify the effect of intervention. For example, being a smoker may be a strong predictor of mortality within the next ten years, but there may not be reason for it to influence the effect of a drug therapy on mortality (Deeks 1998). Potential effect modifiers may include participant characteristics (age, setting), the precise interventions (dose of active intervention, choice of comparison intervention), how the study was done (length of follow-up) or methodology (design and quality).
10.11.5.5 Be aware that the effect of a characteristic may not always be identified
Many characteristics that might have important effects on how well an intervention works cannot be investigated using subgroup analysis or meta-regression. These are characteristics of participants that might vary substantially within studies, but that can only be summarized at the level of the study. An example is age. Consider a collection of clinical trials involving adults ranging from 18 to 60 years old. There may be a strong relationship between age and intervention effect that is apparent within each study. However, if the mean ages for the trials are similar, then no relationship will be apparent by looking at trial mean ages and trial-level effect estimates. The problem is one of aggregating individuals’ results and is variously known as aggregation bias, ecological bias or the ecological fallacy (Morgenstern 1982, Greenland 1987, Berlin et al 2002). It is even possible for the direction of the relationship across studies be the opposite of the direction of the relationship observed within each study.
10.11.5.6 Think about whether the characteristic is closely related to another characteristic (confounded)
The problem of ‘confounding’ complicates interpretation of subgroup analyses and meta-regressions and can lead to incorrect conclusions. Two characteristics are confounded if their influences on the intervention effect cannot be disentangled. For example, if those studies implementing an intensive version of a therapy happened to be the studies that involved patients with more severe disease, then one cannot tell which aspect is the cause of any difference in effect estimates between these studies and others. In meta-regression, co-linearity between potential effect modifiers leads to similar difficulties (Berlin and Antman 1994). Computing correlations between study characteristics will give some information about which study characteristics may be confounded with each other.
10.11.6 Interpretation of subgroup analyses and meta-regressions
Appropriate interpretation of subgroup analyses and meta-regressions requires caution (Oxman and Guyatt 1992).
-
Subgroup comparisons are observational. It must be remembered that subgroup analyses and meta-regressions are entirely observational in their nature. These analyses investigate differences between studies. Even if individuals are randomized to one group or other within a clinical trial, they are not randomized to go in one trial or another. Hence, subgroup analyses suffer the limitations of any observational investigation, including possible bias through confounding by other study-level characteristics. Furthermore, even a genuine difference between subgroups is not necessarily due to the classification of the subgroups. As an example, a subgroup analysis of bone marrow transplantation for treating leukaemia might show a strong association between the age of a sibling donor and the success of the transplant. However, this probably does not mean that the age of donor is important. In fact, the age of the recipient is probably a key factor and the subgroup finding would simply be due to the strong association between the age of the recipient and the age of their sibling.
-
Was the analysis pre-specified or post hoc? Authors should state whether subgroup analyses were pre-specified or undertaken after the results of the studies had been compiled (post hoc). More reliance may be placed on a subgroup analysis if it was one of a small number of pre-specified analyses. Performing numerous post-hoc subgroup analyses to explain heterogeneity is a form of data dredging. Data dredging is condemned because it is usually possible to find an apparent, but false, explanation for heterogeneity by considering lots of different characteristics.
-
Is there indirect evidence in support of the findings? Differences between subgroups should be clinically plausible and supported by other external or indirect evidence, if they are to be convincing.
-
Is the magnitude of the difference practically important? If the magnitude of a difference between subgroups will not result in different recommendations for different subgroups, then it may be better to present only the overall analysis results.
-
Is there a statistically significant difference between subgroups? To establish whether there is a different effect of an intervention in different situations, the magnitudes of effects in different subgroups should be compared directly with each other. In particular, statistical significance of the results within separate subgroup analyses should not be compared (see Section 10.11.3.1).
- Are analyses looking at within-study or between-study relationships? For patient and intervention characteristics, differences in subgroups that are observed within studies are more reliable than analyses of subsets of studies. If such within-study relationships are replicated across studies then this adds confidence to the findings.
10.11.7 Investigating the effect of underlying risk
One potentially important source of heterogeneity among a series of studies is when the underlying average risk of the outcome event varies between the studies. The underlying risk of a particular event may be viewed as an aggregate measure of case-mix factors such as age or disease severity. It is generally measured as the observed risk of the event in the comparator group of each study (the comparator group risk, or CGR). The notion is controversial in its relevance to clinical practice since underlying risk represents a summary of both known and unknown risk factors. Problems also arise because comparator group risk will depend on the length of follow-up, which often varies across studies. However, underlying risk has received particular attention in meta-analysis because the information is readily available once dichotomous data have been prepared for use in meta-analyses. Sharp provides a full discussion of the topic (Sharp 2001).
Intuition would suggest that participants are more or less likely to benefit from an effective intervention according to their risk status. However, the relationship between underlying risk and intervention effect is a complicated issue. For example, suppose an intervention is equally beneficial in the sense that for all patients it reduces the risk of an event, say a stroke, to 80% of the underlying risk. Then it is not equally beneficial in terms of absolute differences in risk in the sense that it reduces a 50% stroke rate by 10 percentage points to 40% (number needed to treat=10), but a 20% stroke rate by 4 percentage points to 16% (number needed to treat=25).
Use of different summary statistics (risk ratio, odds ratio and risk difference) will demonstrate different relationships with underlying risk. Summary statistics that show close to no relationship with underlying risk are generally preferred for use in meta-analysis (see Section 10.4.3).
Investigating any relationship between effect estimates and the comparator group risk is also complicated by a technical phenomenon known as regression to the mean. This arises because the comparator group risk forms an integral part of the effect estimate. A high risk in a comparator group, observed entirely by chance, will on average give rise to a higher than expected effect estimate, and vice versa. This phenomenon results in a false correlation between effect estimates and comparator group risks. There are methods, which require sophisticated software, that correct for regression to the mean (McIntosh 1996, Thompson et al 1997). These should be used for such analyses, and statistical expertise is recommended.
10.11.8 Dose-response analyses
The principles of meta-regression can be applied to the relationships between intervention effect and dose (commonly termed dose-response), treatment intensity or treatment duration (Greenland and Longnecker 1992, Berlin et al 1993). Conclusions about differences in effect due to differences in dose (or similar factors) are on stronger ground if participants are randomized to one dose or another within a study and a consistent relationship is found across similar studies. While authors should consider these effects, particularly as a possible explanation for heterogeneity, they should be cautious about drawing conclusions based on between-study differences. Authors should be particularly cautious about claiming that a dose-response relationship does not exist, given the low power of many meta-regression analyses to detect genuine relationships.
10.12 Missing data
10.12.1 Types of missing data
There are many potential sources of missing data in a systematic review or meta-analysis (see Table 10.12.a). For example, a whole study may be missing from the review, an outcome may be missing from a study, summary data may be missing for an outcome, and individual participants may be missing from the summary data. Here we discuss a variety of potential sources of missing data, highlighting where more detailed discussions are available elsewhere in the Handbook.
Whole studies may be missing from a review because they are never published, are published in obscure places, are rarely cited, or are inappropriately indexed in databases. Thus, review authors should always be aware of the possibility that they have failed to identify relevant studies. There is a strong possibility that such studies are missing because of their ‘uninteresting’ or ‘unwelcome’ findings (that is, in the presence of publication bias). This problem is discussed at length in Chapter 13. Details of comprehensive search methods are provided in Chapter 4.
Some studies might not report any information on outcomes of interest to the review. For example, there may be no information on quality of life, or on serious adverse effects. It is often difficult to determine whether this is because the outcome was not measured or because the outcome was not reported. Furthermore, failure to report that outcomes were measured may be dependent on the unreported results (selective outcome reporting bias; see Chapter 7, Section 7.2.3.3). Similarly, summary data for an outcome, in a form that can be included in a meta-analysis, may be missing. A common example is missing standard deviations (SDs) for continuous outcomes. This is often a problem when change-from-baseline outcomes are sought. We discuss imputation of missing SDs in Chapter 6, Section 6.5.2.8. Other examples of missing summary data are missing sample sizes (particularly those for each intervention group separately), numbers of events, standard errors, follow-up times for calculating rates, and sufficient details of time-to-event outcomes. Inappropriate analyses of studies, for example of cluster-randomized and crossover trials, can lead to missing summary data. It is sometimes possible to approximate the correct analyses of such studies, for example by imputing correlation coefficients or SDs, as discussed in Chapter 23, Section 23.1, for cluster-randomized studies and Chapter 23,Section 23.2, for crossover trials. As a general rule, most methodologists believe that missing summary data (e.g. ‘no usable data’) should not be used as a reason to exclude a study from a systematic review. It is more appropriate to include the study in the review, and to discuss the potential implications of its absence from a meta-analysis.
It is likely that in some, if not all, included studies, there will be individuals missing from the reported results. Review authors are encouraged to consider this problem carefully (see MECIR Box 10.12.a). We provide further discussion of this problem in Section 10.12.3; see also Chapter 8, Section 8.5.
Missing data can also affect subgroup analyses. If subgroup analyses or meta-regressions are planned (see Section 10.11), they require details of the study-level characteristics that distinguish studies from one another. If these are not available for all studies, review authors should consider asking the study authors for more information.
Table 10.12.a Types of missing data in a meta-analysis
|
Type of missing data |
Some possible reasons for missing data |
|
Missing studies |
Publication bias Search not sufficiently comprehensive |
|
Missing outcomes |
Outcome not measured Selective reporting bias |
|
Missing summary data |
Selective reporting bias Incomplete reporting |
|
Missing individuals |
Lack of intention-to-treat analysis Attrition from the study Selective reporting bias |
|
Missing study-level characteristics (for subgroup analysis or meta-regression) |
Characteristic not measured Incomplete reporting |
MECIR Box 10.12.a Relevant expectations for conduct of intervention reviews
|
Consider the implications of missing outcome data from individual participants (due to losses to follow-up or exclusions from analysis). |
Incomplete outcome data can introduce bias. In most circumstances, authors should follow the principles of intention-to-treat analyses as far as possible (this may not be appropriate for adverse effects or if trying to demonstrate equivalence). Risk of bias due to incomplete outcome data is addressed in the Cochrane risk-of-bias tool. However, statistical analyses and careful interpretation of results are additional ways in which the issue can be addressed by review authors. Imputation methods can be considered (accompanied by, or in the form of, sensitivity analyses). |
10.12.2 General principles for dealing with missing data
There is a large literature of statistical methods for dealing with missing data. Here we briefly review some key concepts and make some general recommendations for Cochrane Review authors. It is important to think why data may be missing. Statisticians often use the terms ‘missing at random’ and ‘not missing at random’ to represent different scenarios.
Data are said to be ‘missing at random’ if the fact that they are missing is unrelated to actual values of the missing data. For instance, if some quality-of-life questionnaires were lost in the postal system, this would be unlikely to be related to the quality of life of the trial participants who completed the forms. In some circumstances, statisticians distinguish between data ‘missing at random’ and data ‘missing completely at random’, although in the context of a systematic review the distinction is unlikely to be important. Data that are missing at random may not be important. Analyses based on the available data will often be unbiased, although based on a smaller sample size than the original data set.
Data are said to be ‘not missing at random’ if the fact that they are missing is related to the actual missing data. For instance, in a depression trial, participants who had a relapse of depression might be less likely to attend the final follow-up interview, and more likely to have missing outcome data. Such data are ‘non-ignorable’ in the sense that an analysis of the available data alone will typically be biased. Publication bias and selective reporting bias lead by definition to data that are ‘not missing at random’, and attrition and exclusions of individuals within studies often do as well.
The principal options for dealing with missing data are:
- analysing only the available data (i.e. ignoring the missing data);
- imputing the missing data with replacement values, and treating these as if they were observed (e.g. last observation carried forward, imputing an assumed outcome such as assuming all were poor outcomes, imputing the mean, imputing based on predicted values from a regression analysis);
- imputing the missing data and accounting for the fact that these were imputed with uncertainty (e.g. multiple imputation, simple imputation methods (as point 2) with adjustment to the standard error); and
- using statistical models to allow for missing data, making assumptions about their relationships with the available data.
Option 2 is practical in most circumstances and very commonly used in systematic reviews. However, it fails to acknowledge uncertainty in the imputed values and results, typically, in confidence intervals that are too narrow. Options 3 and 4 would require involvement of a knowledgeable statistician.
Five general recommendations for dealing with missing data in Cochrane Reviews are as follows:
- Whenever possible, contact the original investigators to request missing data.
- Make explicit the assumptions of any methods used to address missing data: for example, that the data are assumed missing at random, or that missing values were assumed to have a particular value such as a poor outcome.
- Follow the guidance in Chapter 8 to assess risk of bias due to missing outcome data in randomized trials.
- Perform sensitivity analyses to assess how sensitive results are to reasonable changes in the assumptions that are made (see Section 10.14).
- Address the potential impact of missing data on the findings of the review in the Discussion section.
10.12.3 Dealing with missing outcome data from individual participants
Review authors may undertake sensitivity analyses to assess the potential impact of missing outcome data, based on assumptions about the relationship between missingness in the outcome and its true value. Several methods are available (Akl et al 2015). For dichotomous outcomes, Higgins and colleagues propose a strategy involving different assumptions about how the risk of the event among the missing participants differs from the risk of the event among the observed participants, taking account of uncertainty introduced by the assumptions (Higgins et al 2008a). Akl and colleagues propose a suite of simple imputation methods, including a similar approach to that of Higgins and colleagues based on relative risks of the event in missing versus observed participants. Similar ideas can be applied to continuous outcome data (Ebrahim et al 2013, Ebrahim et al 2014). Particular care is required to avoid double counting events, since it can be unclear whether reported numbers of events in trial reports apply to the full randomized sample or only to those who did not drop out (Akl et al 2016).
Although there is a tradition of implementing ‘worst case’ and ‘best case’ analyses clarifying the extreme boundaries of what is theoretically possible, such analyses may not be informative for the most plausible scenarios (Higgins et al 2008a).
10.13 Bayesian approaches to meta-analysis
Bayesian statistics is an approach to statistics based on a different philosophy from that which underlies significance tests and confidence intervals. It is essentially about updating of evidence. In a Bayesian analysis, initial uncertainty is expressed through a prior distribution about the quantities of interest. Current data and assumptions concerning how they were generated are summarized in the likelihood. The posterior distribution for the quantities of interest can then be obtained by combining the prior distribution and the likelihood. The likelihood summarizes both the data from studies included in the meta-analysis (for example, 2×2 tables from randomized trials) and the meta-analysis model (for example, assuming a fixed effect or random effects). The result of the analysis is usually presented as a point estimate and 95% credible interval from the posterior distribution for each quantity of interest, which look much like classical estimates and confidence intervals. Potential advantages of Bayesian analyses are summarized in Box 10.13.a. Bayesian analysis may be performed using WinBUGS software (Smith et al 1995, Lunn et al 2000), within R (Röver 2017), or – for some applications – using standard meta-regression software with a simple trick (Rhodes et al 2016).
A difference between Bayesian analysis and classical meta-analysis is that the interpretation is directly in terms of belief: a 95% credible interval for an odds ratio is that region in which we believe the odds ratio to lie with probability 95%. This is how many practitioners actually interpret a classical confidence interval, but strictly in the classical framework the 95% refers to the long-term frequency with which 95% intervals contain the true value. The Bayesian framework also allows a review author to calculate the probability that the odds ratio has a particular range of values, which cannot be done in the classical framework. For example, we can determine the probability that the odds ratio is less than 1 (which might indicate a beneficial effect of an experimental intervention), or that it is no larger than 0.8 (which might indicate a clinically important effect). It should be noted that these probabilities are specific to the choice of the prior distribution. Different meta-analysts may analyse the same data using different prior distributions and obtain different results. It is therefore important to carry out sensitivity analyses to investigate how the results depend on any assumptions made.
In the context of a meta-analysis, prior distributions are needed for the particular intervention effect being analysed (such as the odds ratio or the mean difference) and – in the context of a random-effects meta-analysis – on the amount of heterogeneity among intervention effects across studies. Prior distributions may represent subjective belief about the size of the effect, or may be derived from sources of evidence not included in the meta-analysis, such as information from non-randomized studies of the same intervention or from randomized trials of other interventions. The width of the prior distribution reflects the degree of uncertainty about the quantity. When there is little or no information, a ‘non-informative’ prior can be used, in which all values across the possible range are equally likely.
Most Bayesian meta-analyses use non-informative (or very weakly informative) prior distributions to represent beliefs about intervention effects, since many regard it as controversial to combine objective trial data with subjective opinion. However, prior distributions are increasingly used for the extent of among-study variation in a random-effects analysis. This is particularly advantageous when the number of studies in the meta-analysis is small, say fewer than five or ten. Libraries of data-based prior distributions are available that have been derived from re-analyses of many thousands of meta-analyses in the Cochrane Database of Systematic Reviews (Turner et al 2012).
Box 10.13.a Some potential advantages of Bayesian meta-analysis
|
Some potential advantages of Bayesian approaches over classical methods for meta-analyses are that they:
|
Statistical expertise is strongly recommended for review authors who wish to carry out Bayesian analyses. There are several good texts (Sutton et al 2000, Sutton and Abrams 2001, Spiegelhalter et al 2004).
10.14 Sensitivity analyses
The process of undertaking a systematic review involves a sequence of decisions. Whilst many of these decisions are clearly objective and non-contentious, some will be somewhat arbitrary or unclear. For instance, if eligibility criteria involve a numerical value, the choice of value is usually arbitrary: for example, defining groups of older people may reasonably have lower limits of 60, 65, 70 or 75 years, or any value in between. Other decisions may be unclear because a study report fails to include the required information. Some decisions are unclear because the included studies themselves never obtained the information required: for example, the outcomes of those who were lost to follow-up. Further decisions are unclear because there is no consensus on the best statistical method to use for a particular problem.
It is highly desirable to prove that the findings from a systematic review are not dependent on such arbitrary or unclear decisions by using sensitivity analysis (see MECIR Box 10.14.a). A sensitivity analysis is a repeat of the primary analysis or meta-analysis in which alternative decisions or ranges of values are substituted for decisions that were arbitrary or unclear. For example, if the eligibility of some studies in the meta-analysis is dubious because they do not contain full details, sensitivity analysis may involve undertaking the meta-analysis twice: the first time including all studies and, second, including only those that are definitely known to be eligible. A sensitivity analysis asks the question, ‘Are the findings robust to the decisions made in the process of obtaining them?’
MECIR Box 10.14.a Relevant expectations for conduct of intervention reviews
|
C71: Sensitivity analysis (Highly desirable) |
|
|
Use sensitivity analyses to assess the robustness of results, such as the impact of notable assumptions, imputed data, borderline decisions and studies at high risk of bias. |
It is important to be aware when results are robust, since the strength of the conclusion may be strengthened or weakened. |
There are many decision nodes within the systematic review process that can generate a need for a sensitivity analysis. Examples include:
Searching for studies:
- Should abstracts whose results cannot be confirmed in subsequent publications be included in the review?
Eligibility criteria:
- Characteristics of participants: where a majority but not all people in a study meet an age range, should the study be included?
- Characteristics of the intervention: what range of doses should be included in the meta-analysis?
- Characteristics of the comparator: what criteria are required to define usual care to be used as a comparator group?
- Characteristics of the outcome: what time point or range of time points are eligible for inclusion?
- Study design: should blinded and unblinded outcome assessment be included, or should study inclusion be restricted by other aspects of methodological criteria?
What data should be analysed?
- Time-to-event data: what assumptions of the distribution of censored data should be made?
- Continuous data: where standard deviations are missing, when and how should they be imputed? Should analyses be based on change scores or on post-intervention values?
- Ordinal scales: what cut-point should be used to dichotomize short ordinal scales into two groups?
- Cluster-randomized trials: what values of the intraclass correlation coefficient should be used when trial analyses have not been adjusted for clustering?
- Crossover trials: what values of the within-subject correlation coefficient should be used when this is not available in primary reports?
- All analyses: what assumptions should be made about missing outcomes? Should adjusted or unadjusted estimates of intervention effects be used?
Analysis methods:
- Should fixed-effect or random-effects methods be used for the analysis?
- For dichotomous outcomes, should odds ratios, risk ratios or risk differences be used?
- For continuous outcomes, where several scales have assessed the same dimension, should results be analysed as a standardized mean difference across all scales or as mean differences individually for each scale?
Some sensitivity analyses can be pre-specified in the study protocol, but many issues suitable for sensitivity analysis are only identified during the review process where the individual peculiarities of the studies under investigation are identified. When sensitivity analyses show that the overall result and conclusions are not affected by the different decisions that could be made during the review process, the results of the review can be regarded with a higher degree of certainty. Where sensitivity analyses identify particular decisions or missing information that greatly influence the findings of the review, greater resources can be deployed to try and resolve uncertainties and obtain extra information, possibly through contacting trial authors and obtaining individual participant data. If this cannot be achieved, the results must be interpreted with an appropriate degree of caution. Such findings may generate proposals for further investigations and future research.
Reporting of sensitivity analyses in a systematic review may best be done by producing a summary table. Rarely is it informative to produce individual forest plots for each sensitivity analysis undertaken.
Sensitivity analyses are sometimes confused with subgroup analysis. Although some sensitivity analyses involve restricting the analysis to a subset of the totality of studies, the two methods differ in two ways. First, sensitivity analyses do not attempt to estimate the effect of the intervention in the group of studies removed from the analysis, whereas in subgroup analyses, estimates are produced for each subgroup. Second, in sensitivity analyses, informal comparisons are made between different ways of estimating the same thing, whereas in subgroup analyses, formal statistical comparisons are made across the subgroups.
10.15 Chapter information
Editors: Jonathan J Deeks, Julian PT Higgins, Douglas G Altman; on behalf of the Cochrane Statistical Methods Group
Contributing authors: Douglas Altman, Deborah Ashby, Jacqueline Birks, Michael Borenstein, Marion Campbell, Jonathan Deeks, Matthias Egger, Julian Higgins, Joseph Lau, Keith O’Rourke, Gerta Rücker, Rob Scholten, Jonathan Sterne, Simon Thompson, Anne Whitehead
Acknowledgements: We are grateful to the following for commenting helpfully on earlier drafts: Bodil Als-Nielsen, Deborah Ashby, Jesse Berlin, Joseph Beyene, Jacqueline Birks, Michael Bracken, Marion Campbell, Chris Cates, Wendong Chen, Mike Clarke, Albert Cobos, Esther Coren, Francois Curtin, Roberto D’Amico, Keith Dear, Heather Dickinson, Diana Elbourne, Simon Gates, Paul Glasziou, Christian Gluud, Peter Herbison, Sally Hollis, David Jones, Steff Lewis, Tianjing Li, Joanne McKenzie, Philippa Middleton, Nathan Pace, Craig Ramsey, Keith O’Rourke, Rob Scholten, Guido Schwarzer, Jack Sinclair, Jonathan Sterne, Simon Thompson, Andy Vail, Clarine van Oel, Paula Williamson and Fred Wolf.
Funding: JJD received support from the National Institute for Health Research (NIHR) Birmingham Biomedical Research Centre at the University Hospitals Birmingham NHS Foundation Trust and the University of Birmingham. JPTH is a member of the NIHR Biomedical Research Centre at University Hospitals Bristol NHS Foundation Trust and the University of Bristol. JPTH received funding from National Institute for Health Research Senior Investigator award NF-SI-0617-10145. The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR or the Department of Health.
10.16 References
Agresti A. An Introduction to Categorical Data Analysis. New York (NY): John Wiley & Sons; 1996.
Akl EA, Kahale LA, Agoritsas T, Brignardello-Petersen R, Busse JW, Carrasco-Labra A, Ebrahim S, Johnston BC, Neumann I, Sola I, Sun X, Vandvik P, Zhang Y, Alonso-Coello P, Guyatt G. Handling trial participants with missing outcome data when conducting a meta-analysis: a systematic survey of proposed approaches. Systematic Reviews 2015; 4: 98.
Akl EA, Kahale LA, Ebrahim S, Alonso-Coello P, Schünemann HJ, Guyatt GH. Three challenges described for identifying participants with missing data in trials reports, and potential solutions suggested to systematic reviewers. Journal of Clinical Epidemiology 2016; 76: 147-154.
Altman DG, Bland JM. Detecting skewness from summary information. BMJ 1996; 313: 1200.
Anzures-Cabrera J, Sarpatwari A, Higgins JPT. Expressing findings from meta-analyses of continuous outcomes in terms of risks. Statistics in Medicine 2011; 30: 2967-2985.
Berlin JA, Longnecker MP, Greenland S. Meta-analysis of epidemiologic dose-response data. Epidemiology 1993; 4: 218-228.
Berlin JA, Antman EM. Advantages and limitations of metaanalytic regressions of clinical trials data. Online Journal of Current Clinical Trials 1994; Doc No 134.
Berlin JA, Santanna J, Schmid CH, Szczech LA, Feldman KA, Group A-LAITS. Individual patient- versus group-level data meta-regressions for the investigation of treatment effect modifiers: ecological bias rears its ugly head. Statistics in Medicine 2002; 21: 371-387.
Borenstein M, Hedges LV, Higgins JPT, Rothstein HR. A basic introduction to fixed-effect and random-effects models for meta-analysis. Research Synthesis Methods 2010; 1: 97-111.
Borenstein M, Higgins JPT. Meta-analysis and subgroups. Prev Sci 2013; 14: 134-143.
Bradburn MJ, Deeks JJ, Berlin JA, Russell Localio A. Much ado about nothing: a comparison of the performance of meta-analytical methods with rare events. Statistics in Medicine 2007; 26: 53-77.
Chinn S. A simple method for converting an odds ratio to effect size for use in meta-analysis. Statistics in Medicine 2000; 19: 3127-3131.
da Costa BR, Nuesch E, Rutjes AW, Johnston BC, Reichenbach S, Trelle S, Guyatt GH, Jüni P. Combining follow-up and change data is valid in meta-analyses of continuous outcomes: a meta-epidemiological study. Journal of Clinical Epidemiology 2013; 66: 847-855.
Deeks JJ. Systematic reviews of published evidence: Miracles or minefields? Annals of Oncology 1998; 9: 703-709.
Deeks JJ, Altman DG, Bradburn MJ. Statistical methods for examining heterogeneity and combining results from several studies in meta-analysis. In: Egger M, Davey Smith G, Altman DG, editors. Systematic Reviews in Health Care: Meta-analysis in Context. 2nd edition ed. London (UK): BMJ Publication Group; 2001. p. 285-312.
Deeks JJ. Issues in the selection of a summary statistic for meta-analysis of clinical trials with binary outcomes. Statistics in Medicine 2002; 21: 1575-1600.
DerSimonian R, Laird N. Meta-analysis in clinical trials. Controlled Clinical Trials 1986; 7: 177-188.
DiGuiseppi C, Higgins JPT. Interventions for promoting smoke alarm ownership and function. Cochrane Database of Systematic Reviews 2001; 2: CD002246.
Ebrahim S, Akl EA, Mustafa RA, Sun X, Walter SD, Heels-Ansdell D, Alonso-Coello P, Johnston BC, Guyatt GH. Addressing continuous data for participants excluded from trial analysis: a guide for systematic reviewers. Journal of Clinical Epidemiology 2013; 66: 1014-1021 e1011.
Ebrahim S, Johnston BC, Akl EA, Mustafa RA, Sun X, Walter SD, Heels-Ansdell D, Alonso-Coello P, Guyatt GH. Addressing continuous data measured with different instruments for participants excluded from trial analysis: a guide for systematic reviewers. Journal of Clinical Epidemiology 2014; 67: 560-570.
Efthimiou O. Practical guide to the meta-analysis of rare events. Evidence-Based Mental Health 2018; 21: 72-76.
Egger M, Davey Smith G, Schneider M, Minder C. Bias in meta-analysis detected by a simple, graphical test. BMJ 1997; 315: 629-634.
Engels EA, Schmid CH, Terrin N, Olkin I, Lau J. Heterogeneity and statistical significance in meta-analysis: an empirical study of 125 meta-analyses. Statistics in Medicine 2000; 19: 1707-1728.
Greenland S, Robins JM. Estimation of a common effect parameter from sparse follow-up data. Biometrics 1985; 41: 55-68.
Greenland S. Quantitative methods in the review of epidemiologic literature. Epidemiologic Reviews 1987; 9: 1-30.
Greenland S, Longnecker MP. Methods for trend estimation from summarized dose-response data, with applications to meta-analysis. American Journal of Epidemiology 1992; 135: 1301-1309.
Guevara JP, Berlin JA, Wolf FM. Meta-analytic methods for pooling rates when follow-up duration varies: a case study. BMC Medical Research Methodology 2004; 4: 17.
Hartung J, Knapp G. A refined method for the meta-analysis of controlled clinical trials with binary outcome. Statistics in Medicine 2001; 20: 3875-3889.
Hasselblad V, McCrory DC. Meta-analytic tools for medical decision making: A practical guide. Medical Decision Making 1995; 15: 81-96.
Higgins JPT, Thompson SG. Quantifying heterogeneity in a meta-analysis. Statistics in Medicine 2002; 21: 1539-1558.
Higgins JPT, Thompson SG, Deeks JJ, Altman DG. Measuring inconsistency in meta-analyses. BMJ 2003; 327: 557-560.
Higgins JPT, Thompson SG. Controlling the risk of spurious findings from meta-regression. Statistics in Medicine 2004; 23: 1663-1682.
Higgins JPT, White IR, Wood AM. Imputation methods for missing outcome data in meta-analysis of clinical trials. Clinical Trials 2008a; 5: 225-239.
Higgins JPT, White IR, Anzures-Cabrera J. Meta-analysis of skewed data: combining results reported on log-transformed or raw scales. Statistics in Medicine 2008b; 27: 6072-6092.
Higgins JPT, Thompson SG, Spiegelhalter DJ. A re-evaluation of random-effects meta-analysis. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2009; 172: 137-159.
Kjaergard LL, Villumsen J, Gluud C. Reported methodologic quality and discrepancies between large and small randomized trials in meta-analyses. Annals of Internal Medicine 2001; 135: 982-989.
Langan D, Higgins JPT, Simmonds M. An empirical comparison of heterogeneity variance estimators in 12 894 meta-analyses. Research Synthesis Methods 2015; 6: 195-205.
Langan D, Higgins JPT, Simmonds M. Comparative performance of heterogeneity variance estimators in meta-analysis: a review of simulation studies. Research Synthesis Methods 2017; 8: 181-198.
Langan D, Higgins JPT, Jackson D, Bowden J, Veroniki AA, Kontopantelis E, Viechtbauer W, Simmonds M. A comparison of heterogeneity variance estimators in simulated random-effects meta-analyses. Research Synthesis Methods 2019; 10: 83-98.
Lewis S, Clarke M. Forest plots: trying to see the wood and the trees. BMJ 2001; 322: 1479-1480.
Lunn DJ, Thomas A, Best N, Spiegelhalter D. WinBUGS - A Bayesian modelling framework: Concepts, structure, and extensibility. Statistics and Computing 2000; 10: 325-337.
Mantel N, Haenszel W. Statistical aspects of the analysis of data from retrospective studies of disease. Journal of the National Cancer Institute 1959; 22: 719-748.
McIntosh MW. The population risk as an explanatory variable in research synthesis of clinical trials. Statistics in Medicine 1996; 15: 1713-1728.
Morgenstern H. Uses of ecologic analysis in epidemiologic research. American Journal of Public Health 1982; 72: 1336-1344.
Oxman AD, Guyatt GH. A consumers guide to subgroup analyses. Annals of Internal Medicine 1992; 116: 78-84.
Peto R, Collins R, Gray R. Large-scale randomized evidence: large, simple trials and overviews of trials. Journal of Clinical Epidemiology 1995; 48: 23-40.
Poole C, Greenland S. Random-effects meta-analyses are not always conservative. American Journal of Epidemiology 1999; 150: 469-475.
Rhodes KM, Turner RM, White IR, Jackson D, Spiegelhalter DJ, Higgins JPT. Implementing informative priors for heterogeneity in meta-analysis using meta-regression and pseudo data. Statistics in Medicine 2016; 35: 5495-5511.
Rice K, Higgins JPT, Lumley T. A re-evaluation of fixed effect(s) meta-analysis. Journal of the Royal Statistical Society Series A (Statistics in Society) 2018; 181: 205-227.
Riley RD, Higgins JPT, Deeks JJ. Interpretation of random effects meta-analyses. BMJ 2011; 342: d549.
Röver C. Bayesian random-effects meta-analysis using the bayesmeta R package 2017. https://arxiv.org/abs/1711.08683.
Rücker G, Schwarzer G, Carpenter J, Olkin I. Why add anything to nothing? The arcsine difference as a measure of treatment effect in meta-analysis with zero cells. Statistics in Medicine 2009; 28: 721-738.
Sharp SJ. Analysing the relationship between treatment benefit and underlying risk: precautions and practical recommendations. In: Egger M, Davey Smith G, Altman DG, editors. Systematic Reviews in Health Care: Meta-analysis in Context. 2nd edition ed. London (UK): BMJ Publication Group; 2001. p. 176-188.
Sidik K, Jonkman JN. A simple confidence interval for meta-analysis. Statistics in Medicine 2002; 21: 3153-3159.
Simmonds MC, Tierney J, Bowden J, Higgins JPT. Meta-analysis of time-to-event data: a comparison of two-stage methods. Research Synthesis Methods 2011; 2: 139-149.
Sinclair JC, Bracken MB. Clinically useful measures of effect in binary analyses of randomized trials. Journal of Clinical Epidemiology 1994; 47: 881-889.
Smith TC, Spiegelhalter DJ, Thomas A. Bayesian approaches to random-effects meta-analysis: a comparative study. Statistics in Medicine 1995; 14: 2685-2699.
Spiegelhalter DJ, Abrams KR, Myles JP. Bayesian Approaches to Clinical Trials and Health-Care Evaluation. Chichester (UK): John Wiley & Sons; 2004.
Spittal MJ, Pirkis J, Gurrin LC. Meta-analysis of incidence rate data in the presence of zero events. BMC Medical Research Methodology 2015; 15: 42.
Sutton AJ, Abrams KR, Jones DR, Sheldon TA, Song F. Methods for Meta-analysis in Medical Research. Chichester (UK): John Wiley & Sons; 2000.
Sutton AJ, Abrams KR. Bayesian methods in meta-analysis and evidence synthesis. Statistical Methods in Medical Research 2001; 10: 277-303.
Sweeting MJ, Sutton AJ, Lambert PC. What to add to nothing? Use and avoidance of continuity corrections in meta-analysis of sparse data. Statistics in Medicine 2004; 23: 1351-1375.
Thompson SG, Smith TC, Sharp SJ. Investigating underlying risk as a source of heterogeneity in meta-analysis. Statistics in Medicine 1997; 16: 2741-2758.
Thompson SG, Sharp SJ. Explaining heterogeneity in meta-analysis: a comparison of methods. Statistics in Medicine 1999; 18: 2693-2708.
Thompson SG, Higgins JPT. How should meta-regression analyses be undertaken and interpreted? Statistics in Medicine 2002; 21: 1559-1574.
Turner RM, Davey J, Clarke MJ, Thompson SG, Higgins JPT. Predicting the extent of heterogeneity in meta-analysis, using empirical data from the Cochrane Database of Systematic Reviews. International Journal of Epidemiology 2012; 41: 818-827.
Veroniki AA, Jackson D, Viechtbauer W, Bender R, Bowden J, Knapp G, Kuss O, Higgins JPT, Langan D, Salanti G. Methods to estimate the between-study variance and its uncertainty in meta-analysis. Research Synthesis Methods 2016; 7: 55-79.
Whitehead A, Jones NMB. A meta-analysis of clinical trials involving different classifications of response into ordered categories. Statistics in Medicine 1994; 13: 2503-2515.
Yusuf S, Peto R, Lewis J, Collins R, Sleight P. Beta blockade during and after myocardial infarction: an overview of the randomized trials. Progress in Cardiovascular Diseases 1985; 27: 335-371.
Yusuf S, Wittes J, Probstfield J, Tyroler HA. Analysis and interpretation of treatment effects in subgroups of patients in randomized clinical trials. JAMA 1991; 266: 93-98.
